Гос.рег. №01.20.03 02941
Науч. Руководитель: к.ф.-м.н.
А.С.Петросян
Получены точные
решения уравнения Больцмана для турбулентных течений при наличии коагуляции,
испарения и конденсации. Получены уравнения для описания поведения размеров и
скоростей аэрозольных частиц под действием произвольных сил. Найдены некоторорые аналитические решения полученных уравнений.
С.В. Симакин
«Изучение поведения зависимости размеров и скоростей аэрозольных частиц под
действием произвольных сил», Тезисы докладов,
А.Петросян,
333-54-78, apetrosy@iki.rssi.ru
Разработан
метод крупных вихрей для теплопроводящей плазмы. Получены отфильтрованные по Фавру уравнения магнитной гидродинамики проводящего газа с
учетом уравнения энергии. Разработаны новые параметризации для слагаемых,
которые описывают подсеточные явления, вызванные
наличием, как магнитного поля, так и уравнения полной энергии. Осуществлено численное моделирование
вырождающейся сжимаемой магнитогидродинамической турбулентности.
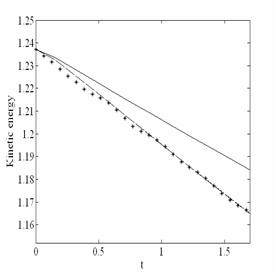
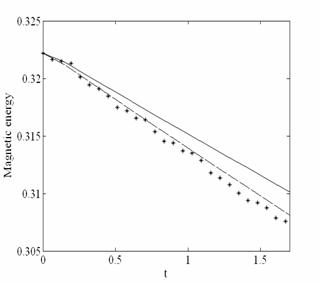
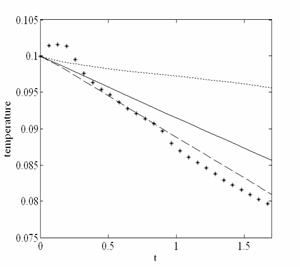
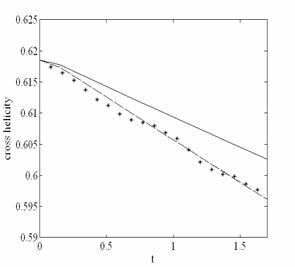
Осуществлено прямое численное моделирование вырождающейся сжимаемой магнитогидродинамической турбулентности для теплопроводящей плазмы. Для этого был использован метод Рунге-Кутта 3го порядка точности для временного интегрирования и 4го порядка точности конечно-разностные схемы для пространственных производных. Проведено сравнение с результатами, полученными методом крупных вихрей. Проведены расчеты и получена временная эволюция для кинетической энергии, для магнитной энергии, для взаимной спиральности магнитного поля и поля скорости и для температуры.
A.A. Chernyshov, K.V. Karelsky, A.S. Petrosyan “Subgrid-scale modelling of compressible magnetohydrodynamic
turbulence in heat-conducting plasma”, Physics of Plasmas, Vol. 13, Issue 10,
104501, 2006
А. Чернышов, 333-54-78, achernyshov@iki.rssi.ru
Исследована вырождающаяся сжимаемая магнитогидродинамическая турбулентность в политропном газе при различных параметрах подобия, а именно, при различных числах гидродинамического Рейнольдса, чисел Маха и магнитного числа Рейнольдса. Проведено сравнение метода крупных вихрей с результатами прямого численного моделирования.
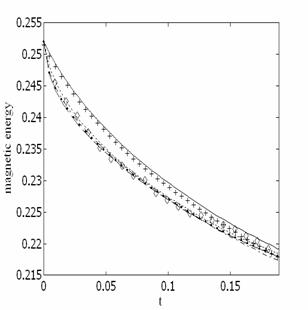
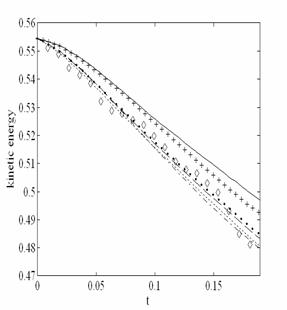
Временная эволюция кинетической и магнитной энергии для случая, когда ![]()
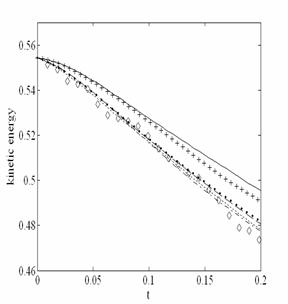
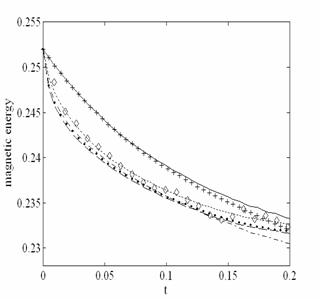
Временная эволюция кинетической и магнитной энергии для случая, когда ![]()
A. A. Chernyshov, K. V. Karelsky, A. S.
Petrosyan «Development of large eddy simulation for
modeling of decaying compressible MHD turbulence», Physics of Fluids, представлена к печати
А. Чернышов, 333-54-78, achernyshov@iki.rssi.ru
Осуществлено трехмерное моделирование переноса аэрозолей в планетарном пограничном слое над неоднородной подстилающей поверхностью. Моделирование осуществлено методом Годунова для трехмерных уравнений идеального газа с переменным уравнением состояния. Показано возможность моделирования среднего течения в пограничном слое на основе модели схемной вязкости, которая обеспечивает диффузию возмущения на твердой границе и выполнимость гипотезы Прандтля. Получены численные расчеты для ветра и распределение твердых аэрозолей в пограничном слое над неровной поверхностью.
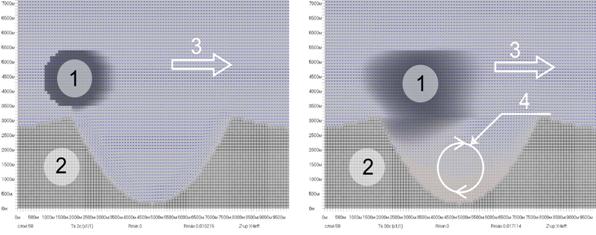
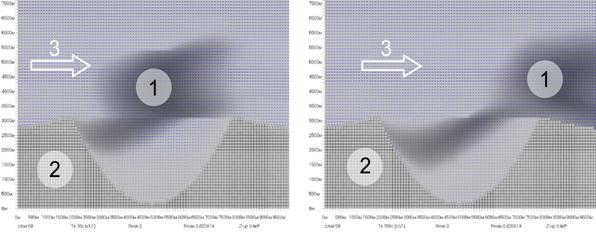
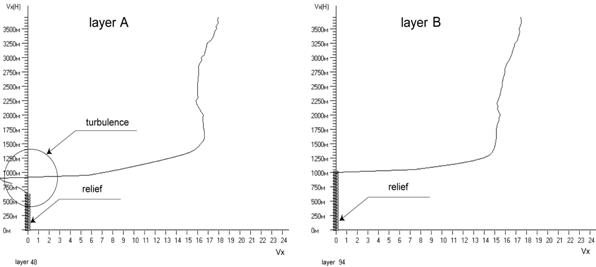
K. Karelsky,
A. Petrosyan, I. Smirnov "A
new model for boundary
layer flows interacting with particulates in land surface on complex terrain.", представлена к печати.
К. Карельский,
333-54-78, kkarelsk@iki.rssi.ru
Разработан
метод расчета течений тяжелой жидкости со свободной поверхностью на
произвольной границе на базе квазидвухслойной модели
мелкой воды для решения задачи Римана. Предложен
вычислительный метод для моделирования течений тяжелой жидкости со свободной
поверхностью над границей произвольной формы. Метод основан на представлении
произвольной границы ступенчатой поверхностью и использовании традиционного
метода Годунова в областях однородной горизонтальной поверхности и специальным
способом расчеты потоковых величин в областях примыкающих к вертикальным
особенностям рельефа дна. Расчет соответствующих потоков ведется на основе квази-двухслойной модели мелкой воды, являющейся уточнением
классической однослойной модели по отношению к исходной системе уравнений
Эйлера. Предложенный численный метод
позволят вести расчет гидродинамических течений тяжелой невязкой жидкости со
свободной поверхностью над произвольным профилем дна. Метод обеспечивает
единообразие построения решения как в
областях со сложной геометрией подстилающей поверхности, так и в областях ровного
дна, экономичность при работе с большими расчетными областями по пространству,
учет диссипации поступательной кинетической энергии, за счет возникающей у
ступеньки турбулентности, и возможность добавления
разнообразных стоков, массовых источников, трения. Работоспособность
метода была проверена моделированием различных гидродинамических задач,
включающих различные особенности подстилающих поверхностей. Показано
соответствие численных результатов
теоретически возможным при аналитическом решении задачи распада произвольно
разрыва над ступенькой, соответствие численных результатов решения задачи над
наклонной плоскостью, аппроксимируемой множеством ступенек, результатам
расчета, использующего решения стандартной задачи Римана и последующей заменой
переменных.
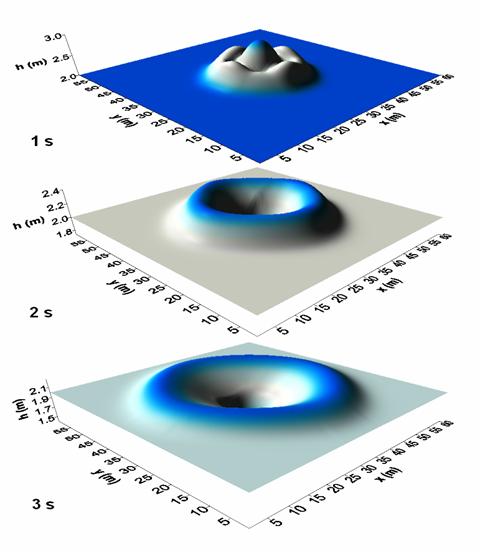
Эволюция падения столба жидкости над
подстилающей поверхностью наполненной жидкостью с выступающим из дна столбом
квадратной формы.

Поток жидкости над
неоднородной подстилающей поверхностью в момент времени 2 с.
К. В. Карельский, А. С. Петросян, А. Г. Славин "Численное моделирование течений невязкой тяжелой жидкости со свободной поверхностью в поле силы тяжести над подстилающей поверхностью произвольного профиля.", Журнал Вычислительной Математики и Математической Физики, представлена к печати.
А. Петросян,
333-54-78, apetrosy@iki.rssi.ru
Получены
уравнения теромхалинной конвекции в неупругом
приближении. Найдено основное состояние, описывающее невозмущенное течение.
Выведено дисперсионное уравнение для малых возмущений.
К. Карельский, 333-54-78, kkarelsk@iki.rssi.ru
Флуктуационные и шумозависимые
процессы в нелинейных системах
Построена нелинейная теория предбифуркационного усиления флуктуаций, описывающая нелинейное насыщение флуктуационных характеристик в непосредственной близости к точке бифуркации.
Построена нелинейная теория предбифуркационного усиления шума, которая описывает нелинейное насыщение флуктуаций в непосредственной близости к точке бифуркации. Показано, что в линейном режиме (вдали от бифуркационного порога) интенсивность флуктуаций пропорциональна дисперсии шума. По мере приближения к порогу бифуркации дисперсия вынужденных флуктуаций растет и в сильно нелинейном режиме (в непосредственной близости к точке бифуркации) достигает насыщения на уровне значения пропорционального среднеквадратичному значению шумовой силы. Рассмотрение проведено на примере бифуркации удвоения периода и на примере нелинейного осциллятора, испытывающего бифуркацию спонтанного нарушения симметрии. Отмечено, что обнаруженные закономерности имеют общий характер.
Показано, что предбифуркационное усиление шума наиболее сильно выражено при медленном прохождении системы через бифуркационную точку, тогда как при быстрых бифуркационных переходах эффект усиления фактически нивелируется.
Обнаружено явление насыщения времени корреляции флуктуаций при приближении к бифуркационному порогу. Показано, что в линейной аппроксимации время корреляции устремляется в бесконечность, тогда как нелинейная теория предсказывает насыщение времени корреляции на уровне, обратно пропорциональном среднеквадратичному значению шума. Показано, что теоретические оценки удовлетворительно согласуются с результатами численного моделирования. Отмечено, что установленные закономерности присущи и другим типам бифуркаций.
Предложен метод оценки флуктуационных характеристик при передаче сообщений с использованием хаотических последовательностей.
Предложены методы измерения интенсивности слабых шумов и обнаружения бифуркаций в нелинейных системах, основанные на явлении предбифуркационного усиления флуктуаций. Указанные методы могут использоваться при обработке временных рядов данных геофизических наблюдений.
д. ф.-м. н. Е. Д. Суровяткина
E.
Surovyatkina and M. Shahin,
New method for signal processing: detecting of bifurcations in time-series of
nonlinear systems, in: Advances in Applied and Computational Mathematics, Nova
Science Publishers,