2.5. Фундаментальные и прикладные научные исследования в области механики, систем управления и информатики

 

Тема УПРАВЛЕНИЕ Исследования в области динамики сложных механических систем, проектирования орбит и построения математических моделей планирования космических экспериментов

Гос. регистрация № 01.20.03 03442

 

Научный руководитель д.т.н. Р.Р. Назиров

 

 

1. Исследование изоморфизма эволюционно зрелых суперэлитных плазменных колец, орбит планетарных и спутниковых систем  и  орбит электронов в Боровской модели атома водорода. Исследование изоморфизма собственного вращения планет как реликтов эволюционно зрелых элитных плазменных колец и квантовых ротаторов бозонного и фермионного типов. Анализ динамики вращающихся КА с МГД-элементом в контуре управления пространственным положением КА при наличии отсеков, частично заполненных жидкостью, и упругой штыревой антенны. Рассмотрение проблемы одноосной и трехосной ориентации КА нового поколения с использованием тороидальных и сферических МГД-элементов. Рассмотрение проблемы использования энергии импульсного магнитного поля для ускорения струи ионизированного газа (холодной плазмы).

Сделан предварительный анализ динамики океана спутника Юпитера Европа совместно с его ледяной оболочкой. Исследование спектра частот гравитационных, гидроупругих и планетарных (гироскопических)  волн в ячейках Томсона – Деланея в ледяной поверхности. Сформулирована задача экспериментального доказательства вращения океана Европы и дано аналитическое решение задачи о вращении океана и ег о ледяной оболочки.

Проведены дальнейшие исследования в области изоморфизма планетарных и спутниковых систем атому водорода. Исследованы адиабатические инварианты Солнечной системы: орбитальный инвариант и спин эквивалентного квантового ротатора.

Проведены дальнейшие исследования по использованию новых физических принципов, а именно, магнитогидродинамических эффектов для управления движущимися объектами. Имеются в виду бесшарнирные системы в контурах ориентации и стабилизации нового поколения КА, не требующие расхода рабочего тела. Эти исследования включают упругие элементы типа штыревых антенн.

      Проведены предварительные исследования, связанные с созданием магнитогидродинамических ракетных двигателей.

 г.н.с. д.ф.-м.н.  Б.И. Рабинович, тел.  333-50-45

 

2. Исследования динамики полета и управления космических аппаратов с солнечным парусом с изменяемой отражательной способностью.  Разработка концепций и алгоритмов управления группировками космических аппаратов при построении и поддержании заданной конфигурации группировок путем использования солнечного паруса с изменяемыми отражательными характеристиками.

 

Разработан метод определения управляющих воздействий на аппараты,
движущиеся в составе группировки около коллинеарных точек либрации.
При этом в качестве исполнительных элементов системы управления
рассмотрены солнечные паруса с изменяемой отражательной способностью.
Показано, что для типичных задач, выполняемых группировками, такой
подход технически реализуем.

 

в.н.с., к.т.н. Эйсмонт Н.А., Тел.  333-10-78, E-mail: neismont@iki.rssi.ru

 

3. Разработка способов управления движения космических приборов, состоящих из элементов, размещаемых на нескольких аппаратах.

 

На основе результатов предыдущего пункта и с учетом конкретных
ограничений проведен анализ возмущений, действующих на аппараты,
движущихся в окрестности коллинеарных солнечно-земных точек либрации
на примере аппаратов проекта XEUS. Показано, что удержание этих
аппаратов в заданном относительном положении возможно с помощью
солнечного паруса с управляемым коэффициентом отражения. При этом
размеры паруса сопоставимы с размерами солнечных батарей аппаратов,
если, как требует эксперимент, расстояния между аппаратами группировки
не превышают 100 - 200 метров. Выпущен препринт с изложением решения
этой задачи.

в.н.с., к.т.н. Эйсмонт Н.А., Тел.  333-10-78, E-mail: neismont@iki.rssi.ru

 

4. Разработка методов управления ориентацией малых космических аппаратов с минимальным составом измерительных и исполнительных элементов, предназначенных для околоземных и межпланетных полетов. Разработка методов управления малыми космическими аппаратами, использующими двигатели малой тяги для решения задач перехода на высокие околоземные орбиты и в межпланетных миссиях, в том числе построение алгоритмов управления ориентацией.

 

В рамках исследования задач управления малыми космическими аппаратами,
в том числе проблем определения ориентации с ограниченным составом
измерений, исследованы алгоритмы управления применительно к аппаратам,
предназначенным для полетов на орбиту спутников Луны. В рамках
возникающих при этом ограничений и требований бортового применения
разработана математическая модель управления движением аппарата,
снабженного электрореактивным двигателем малой тяги. Источником
энергии предполагаются солнечные батареи, постоянно ориентированные на
Солнце, при этом тяга двигателя постоянно направлена вдоль вектора
скорости аппарата. Построен алглритм управления ориентацией аппарата,
позволяющий реализовать соответствующаее движение около центра масс и
наведение батарей на Солнце. С помощью этого алгоритма и упомянутой
модели движения проведено моделирование полета на орбиту спутника
Марса. По результатам работы выпущен препринт.

в.н.с., к.т.н. Эйсмонт Н.А., Тел.  333-10-78, E-mail: neismont@iki.rssi.ru

 

 

5. Разработка системы программ навигацинной поддержки и планирования операций для проекта "Фобос-Грунт" с учетом реализации миссии в режиме взаимодействия с европейским проектом "ExoMars".

 

Проведены подготовительные работы к реализации проекта Фобос-Грунт в
части разработки соответствующего математического обеспечения для получения требуемых научными экспериментами данных и управления приборами. Подговлены предложения по составу работ ЕКА в проекте в том, что касается баллистического обеспечения. Эти предложения рассмотрены и приняты ЕКА.

В дополнение к запланированным работам были проведены исследования по проблеме астероидной опасности и выработаны предложения по методам предотвращения столкновения астероидов с Землей. Эти предложения были изложены на семинаре ИКИ "Механика, информатика и процессы управления".

Кроме того, в рамках подготовки предложений по Восточному Полигону была подготовлена глава по составу и задачам средств запуска космических аппаратов научного назначения.

Подготовлена глава к Дополнению к Эскизному Проекту по СРГ по проблемам выбора и проектирования орбиты, динамики полета и управления орбитальным движением и ориентацией аппарата, а также оптимизации сценария выведения аппарата на рабочую орбиту.

 

в.н.с., к.т.н. Эйсмонт Н.А., Тел.  333-10-78, E-mail: neismont@iki.rssi.ru

 

6. Разработка алгоритмов управления сложными системами в условиях неопределенности. Исследование нестационарных процессов в динамических системах при случайных возмущениях

 

Продолжено исследование нестационарных процессов в динамических системах со слабыми случайными возмущениями. В работах 2006-2007 г. строились асимптотические оценки среднего времени и вероятности выхода из допустимой области для многомерных нелинейных механических систем, заданных уравнениями Лагранжа. Было показано, что в системах с линейной  диссипацией и аддитивным шумом асимптотическая оценка среднего времени пребывания в области может быть получена в явном виде как сумма двух слагаемых, зависящих от кинетической и потенциальной энергии, соответственно.

В работах 2008 г. строятся аналогичные оценки для системы с нелинейной диссипацией [1]. Рассмотрены примеры: (1) найдена оценка среднего времени устойчивого вращения ротора при действии случайной вибрации, вызванной турбулентностью потока жидкости; (2) построена нелинейная система виброзащиты, минимизирующая амплитуду колебаний многоэтажного здания при случайных колебаниях фундамента.

Полученные асимптотические оценки используются для построения законов управления, обеспечивающих желаемые показатели надежности, не зависящие от интенсивности внешнего шума [2] - [4]. Исследована задача управления бетатронными колебаниями частицы; построена система стабилизации гироскопа.

1.     A. Kovaleva. Explicit asymptotic solutions for a class of weak-noise escape problems. Probabilistic Engineering Mechanics, 2009, vol.24, No 1, pp. 84-88 (в печати).

2.     A. Kovaleva. Explicit performance criteria for nonlinear structures. Proceedings of the 4th European Conference on Structural Control, St Petersburg, Russia, September 8-12, 2008. Pp.420-427. 

3.     A. Kovaleva. Dissipative and potential controls guaranteeing noise-independent residence time in weakly perturbed systems. Book of Abstracts of the International Conference “Differential Equations and Topology”, dedicated to the 100 Anniversary of L.S. Pontryagin. Steklov Mathematical Institute RAS and Moscow State University, Moscow, Russia, 17-22 June, 2008. Pp. 260-261.

4.     A. Kovaleva. Control of large deviations in Lagrangian systems with noise-independent residence time. Book of  Abstracts of the 6th Seminar on Stochastic Analysis, Random Fields and Applications, Centro Stefano Franscini, Ascona, Switzerland, May 19-23, 2008. P.31.

УЧАСТИЕ В НАУЧНЫХ КОНФЕРЕНЦИЯХ

1. 3rd International Conference “Smart Materials, Structures and Systems”. Acireale, Sicily, Italy; June 8-13, 2008 (invited).

2. 6th Seminar on Stochastic Analysis, Random Fields and Applications. Centro Stefano Franscini, Ascona, Switzerland; May 19-23, 2008 (invited).

3. International Symposium on Vibro-Impact Dynamics of Ocean Systems and Related Topics. Troy, Michigan, USA; October 2-3, 2008 (invited).

4. International Conference “Differential Equations and Topology”, dedicated to the 100 Anniversary of L.S. Pontryagin. Steklov Mathematical Institute RAS and Moscow State University, Moscow, Russia; June, 17-22б 2008.

5.  4th European Conference on Structural Control. St Petersburg, Russia; September 8-12, 2008.

 

в.н.с.,  д.ф.-м.н.  А. С. Ковалева, a.kovaleva@ru.net

 

7. Дальнейшее исследование особенностей эволюции орбит ИСЗ и времени их существования при совместном влиянии несферичности центрального тела и гравитационных возмущений со стороны внешних тел

 

Рассматривается задача качественного исследование многообразий начальных условий, приводящих (или не приводящих) к пересечению орбиты спутника с поверхностью планеты радиуса R при совместном влиянии гравитационных возмущений от  сжатия планеты и от внешних тел.

Вводится понятие планетоцентрической d-сферы, как области, в которой доминируют гравитационные возмущения от сжатия планеты над  возмущениями от внешних тел.  Радиус  d-сферы соответствует среднему значению радиуса орбиты спутника, при котором отношение возмущающих ускорений от сжатия планеты к возмущающим ускорениям от внешнего тела равно единице. 

Тогда значение параметра бета, определяющего характер эволюции орбиты,  выражается через отношение большой полуоси орбиты спутника к радиусу d-сферы и равно этому отношению, возведенному в степень минус 5.  Значения параметра бета больше единицы внутри d-сферы, равно единице на границе и меньше единицы вне d-сферы. 

Радиус d-сферы является границей, разделяющей значения средних радиусов (больших полуосей) орбит спутников, эволюция которых происходит под преимущественным влиянием того или иного из упомянутых факторов.

Для орбит, большие полуоси которых превышают радиус d-сферы (а значение бета близко к нулю), можно использовать  результаты  многопараметрического анализа долговременной эволюции орбит, полученные для  спутникового варианта интегрируемой двукратно осредненной ограниченной задачи трех тел без учета сжатия планеты. 

В этом случае на множестве возможных значений большой полуоси a0/R, наклонения орбиты спутника к плоскости орбиты возмущающего тела i0, параметра  epsilon0 = 1- e0 ^2 , где e0  значение эксцентриситета, получена следующая классификация многообразий:

многообразие I начальных условий a0/R, i0,  при которых эволюция орбиты спутника приводит к пересечению с поверхностью центрального тела при любых начальных значениях epsilon,  

многообразие II начальных условий a0/R, i0, e0, при которых орбиты спутников не пересекают поверхность центрального тела независимо начальных значений остальных угловых элементов,

многообразие III начальных условий a0/R, i0, e0, при которых орбиты спутников пересекают (или не пересекают) поверхность центрального тела в зависимости от  начальных значений остальных угловых элементов.

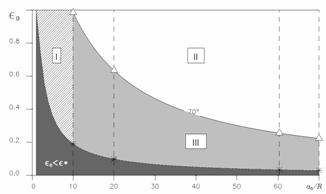
На рисунке, используемом в качестве примера, по оси абсцисс показано отношение большой полуоси к радиусу центрального тела R,  по оси ординат - значение epsilon0, а начальное значение i0 фиксировано и равно 70 градусам. Затемненная область соответствует «запрещенным»  начальным значениям эксцентриситета, при которых радиус перицентра меньше радиуса планеты. 

Для исследования долговременной эволюции орбит, средние радиусы которых не превосходят радиуса d-сферы,  эффективным оказался подход, основанный  на  принципе разделения переменных, с помощью которого удалось получить выражение эксцентриситета в функции времени в форме квадратуры,  выраженной через угловые элементы. Такой подход открывает возможность использования арсенала полученных многими авторами решений, описывающих эволюцию угловых элементов под влиянием возмущений, обусловленных  сжатием планеты, без учета возмущений от третьего тела.

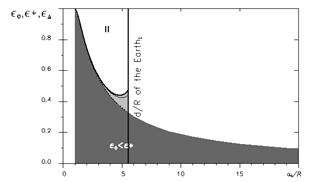
На примере  одного начального значении наклонения орбиты к плоскости экватора планеты ieq0 = 90° показано, как  предложенный алгоритм позволяет найти многообразия типа  II и III в области начальных значений a0/R, e0. Показано также, что с увеличением значения безразмерного радиуса  d/R многообразие III нивелируется и остается только многообразие  II. Аналога многообразию I в этом случае не существует, то есть, для рассматриваемого значения наклонения нет таких значений большой полуоси, при которых эволюция приводит к неизбежному пересечению орбиты спутника с поверхностью центрального тела при любых начальных значениях эксцентриситета.

Заметим, что в задаче связанной с учетом возмущений от сжатия нет того единообразия эволюции орбитальных элементов,  которое свойственно ограниченной двукратно-осредненной задаче трех тел, поэтому для орбит, принадлежащих  d-сфере,  по-видимому,  будет не просто сделать такой же полноты анализ, как для орбит, средние радиусы которых больше радиуса d- сферы. 

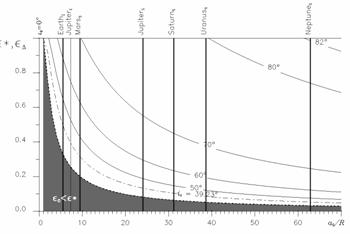
На последнем рисунке для шести планет солнечной системы показаны отнесенные к радиусам планет значения радиусов d- сфер, рассчитанные в системах планета – Солнце – спутник планеты. Для Юпитера показано два значения радиуса d- сферы, меньшее из них, помеченное индексом Sigma, получено при учёте гравитационных  от Солнца и четырех Галилеевых спутников. В качестве фона на этом рисунке показаны границы многообразий начальных условий, полученных для  спутникового варианта интегрируемой двукратно осредненной ограниченной задачи трех тел без учета сжатия планеты (которые действительны только вне d- сфер).    

 

 

1.     Прохоренко В.И. Планетоцентрическая гравитационная сфера доминирующего влияния возмущений  от сжатия планеты над  возмущениями от внешних тел // Космич. Исслед.  2008.  Поступила в редакцию 18 сентября 2008.

2.     Прохоренко В.И. Планетоцентрическая гравитационная сфера доминирующего влияния возмущений  от сжатия планеты над  возмущениями от внешних тел и проблема пересечения орбиты с поверхностью планеты. Доклад на Совете по небесной механике ГАИШ 7 октября 2008.

3.     V. Prokhorenko. Gravitational Sphere of Dominant Perturbations Caused by Planetary Oblatness in Comparison with Perturbations of the Third Body. Proceedings.  International astronomical  meeting “Dynamics of Solar System Bodies” , Tomsk, July 27 –   August 1, 2008.

 

с.н.с. к.ф.-м.н.  В. И. Прохоренко, тел.  333-50-45,   vprokhor@iki.rssi.ru

 

8. Кинематика астероида Апофис в его движении в геоцентрической инерциальной  системе координат

 

Проведено качественное исследование кинематики в геоцентрическом движении астероида (99942) Апофис, тесное сближение которого с Землей ожидается в 2029 году, а затем,  опасное - в 2036. 

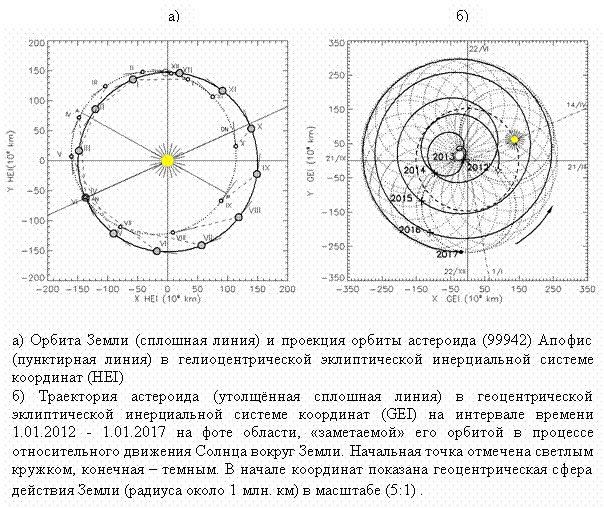
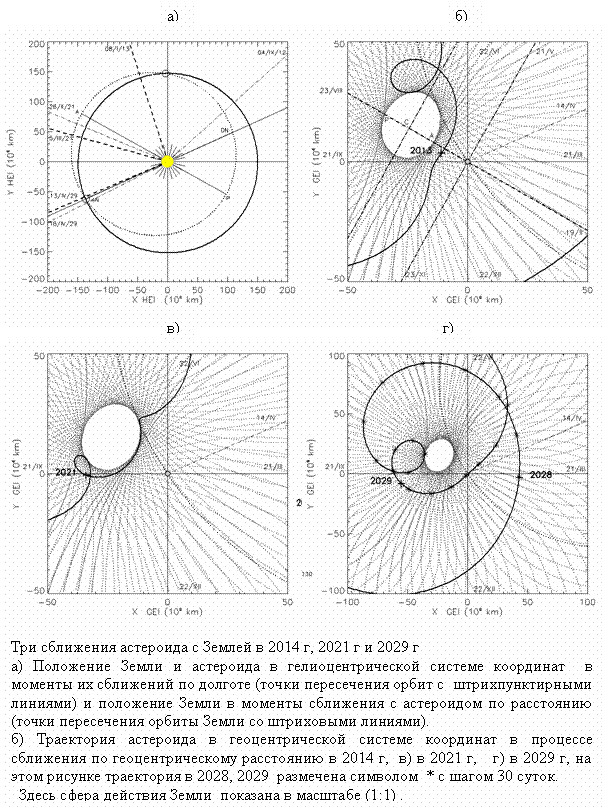
            Согласно данным  JPL Small-Body Database от 2008 г орбита Апофиса имеет большую полуось около 0.92 астрономической единицы (а.е.) (меньше большой полуоси орбиты Земли, равной 1 а.е.), эксцентриситет 0.19, наклонение к плоскости эклиптики составляет  3.3°, аргумент перигелия w = 126.386°   и пересекает орбиту Земли в точке восходящего узла своей орбиты (W = 204. 4479°).

 

На рисунке а) показаны орбиты Земли и астероида в гелиоцентрической эклиптической инерциальной системе координат и положение  каждого из объектов на его орбите в одни и те же моменты времени с дискретностью 1 месяц в течение одного года (2012) размечены номерами месяцев. В каждой точке показано направление скорости. Принадлежащие разным орбитам точки, соответствующие  одинаковым моментам времени соединены  штриховой линией. 

Если перенести начало координат в центр Земли (см. рис. б)), то в этой системе координат движение астероида может быть представлено в виде суммы трех движений: почти кругового движения фокуса его орбиты, расположенного в центре Солнца, поступательного движения орбиты (как целого) и движения астероида по его орбите вокруг Солнца.  На рисунке (б) траектория Апофиса в геоцентрической инерциальной системе координат показана утолщенной сплошной линией, орбита Солнца –  штриховой линией. Пунктирными линиями показаны орбиты астероида, соответствующие различным датам с шагом 15 суток.  Штрихпунктирный луч, отмеченный датой 1/I,  указывает на положение Солнца, которому  соответствует орбита астероида, показанная утолщенной пунктирной линией. Заметим, что на этой кривой лежат отмеченные маркером + точки, через которые проходит траектория астероида первого января каждого года, принадлежащего  рассматриваемому интервалу времени (1.01.2012 - 1.01.2017).

На самом деле, для каждой даты имеется своя кривая, которая является геометрическим местом точек положения астероида на его траектории в геоцентрической инерциальной системе координат  в разные годы, но в одну и туже дату.

В частности, на рис. б) показан луч, соответствующий дате 14 апреля, и соответствующее геометрическое место точек возможного положения астероида (утолщенная пунктирная  линия).  В этом случае геометрическое место точек  проходит через центр Земли. Потенциальная угроза столкновения существует именно в эту дату, если в каком-то году именно в эту дату произойдет сближение астероида с Землей по долготе. 

На этом рисунке показана также свободная от заметания орбитами область, ограниченная  внутренней огибающей заметаемой области. Эта область лежит в окрестности точки C с координатами XC = -24.46 млн. км,   YC = 13.68 млн. км и имеет форму овала, большая полуось которого  равна ~19 млн. км, а малая полуось –  ~ 11.87 млн. км.

Исходя из значений средних движений (угловой скорости движения по орбите вокруг Солнца) астероида  nA = 1.1° в сутки и Земли  nE = 0.98° в сутки,  по формуле  SA = 360°/(nA - nE) рассчитывается синодический период обращения астероида вокруг Солнца SA ~ 7.8 года.  Синодический период характеризует интервал времени, измеряемый между двумя последовательными одноименными конфигурациями (в данном случае сближениями астероида с Землёй по долготе, измеряемой в плоскости эклиптики).

На следующей серии рисунков показаны три прогнозируемых (с периодичностью близкой к синодическому периоду) сближения астероида с Землей, приходящиеся на разные участки орбиты астероида.  На рис. а)  штрихпунктирными линиями показаны даты сближения по эклиптической долготе, а штриховыми утолщенными линиями – даты сближений по геоцентрическому расстоянию. На остальных рисунках в увеличенном масштабе показаны траектории астероида для каждого из трех сближений (по расстоянию).

Отметим, что при сближении 13 апреля 2029 года астероид попадает в сферу действия массивного тела (Земли) и его орбита подвергается значительному гравитационному возмущению при облете Земли.  Для прогноза движения астероида после этого сближения требуется уточнить значения орбитальных элементов  возмущенной орбиты.

 

 

с.н.с. к.ф.-м.н.  В. И. Прохоренко, тел.  333-50-45,   vprokhor@iki.rssi.ru

 

9. Проведение исследований по проекту MetNet создания сети малых метеостанций на Марсе (науч. рук. В.М. Линкин).

 

Был проведен дополнительный анализ траекторий перелета Земля–Марс при выведении КА в 2015 и 2018 гг. на круговую орбиту ИСЗ высотой 600–800 км или орбиту, близкую к рабочей орбите спутника «Молния», и дальнейшем полете с малой тягой. Анализ проводился для четырех вариантов, отличающихся типами и мощностью электрореактивных двигателей (ЭРД) малой тяги. Анализировались следующие участки траектории КА:

       1) Разгон малой тягой по спиральной траектории у Земли и выведение на гелиоцентрическую орбиту. Время разгона варьировалось от минимально возможного (1.5–3 месяца в зависимости от типа и мощности ЭРД) до 1 года. Была получена зависимость расхода рабочего тела от времени разгона.

       2) Перелет Земля–Марс с малой тягой по оптимальной гелиоцентрической траектории.

       3) Торможение малой тягой в сфере действия Марса и выведение КА на ареоцентри-ческую орбиту; торможение малой тягой, как и разгон у Земли, осуществляется по спиральной траектории. Рассматривались 2 варианта: выведение на 2-х и 3-х суточную орбиту спутника Марса. Как и в случае разгона, время торможения варьировалось от минимально возможного (0.5–1 месяц) до года.

       Получены массовые характеристики КА для различных типов и мощностей ЭРД, разных дат полета и всех перечисленных выше вариантов разгона и торможения. Результаты имеются в виде дополнения к отчету 2007 г. и рабочих материалов.

 

с.н.с.,  к.ф.-м.н.  А. А. Суханов, sukhanov@iki.rssi.ru

 

10. Анализ возможности захвата КА в верхней атмосфере планет-гигантов (инициативное исследование)

  

Было завершено начатое в 2007 г. исследование возможности выведения КА на орбиту спутника планеты-гиганта путем торможения в верхних слоях атмосферы планеты. При этом рассматривалась идея уточнения параметров верхней атмосферы непосредственно перед захватом путем сброса с борта КА малых зондов, их входа в атмосферу перед захватом и передачи на борт КА данных о величине торможения зондов в атмосфере на разных высотах. Однако, как показал проведенный в 2007–2008 гг. анализ, предложенная идея не обеспечивает надежного определения параметров верхней атмосферы при небольших затратах и относительно небольшой массе отделяемых зондов и другой необходимой аппаратуры. Поэтому дальнейший анализ предложенной идеи был прекращен. Более перспективной представляется идея активного маневрирования КА в верхних слоях атмосферы планеты-гиганта с целью выбора слоев с подходящей для захвата плотности атмосферы. Однако эта идея требует отдельного исследования с использованием принципиально других методов.

       Результаты исследования представлены в виде рабочих материалов.

 

Сверхплановые работы

 

       1. Проект «Лаплас» (руководитель Л.М. Зеленый).

       Международный проект «Лаплас» предусматривает запуск КА на спутник Юпитера Европа. В рамках этого проекта были выполнены следующие работы:

       1) Найдены и проанализированы оптимальные траектории полета к Юпитеру в 2017–2021 гг., такие как:

       – прямой перелет Земля–Юпитер;

       – Земля–Венера–Земля–Юпитер (два разных варианта);

       – Земля–Венера–Марс–Земля–Юпитер;

       – Земля–активный маневр в афелии–Земля–Юпитер;

       – Земля–Венера–Земля–Земля–Юпитер (в том числе и вариант с активным маневром между двумя облетами Земли).

       2) Проанализированы различные варианты маневрирования КА в сфере действия Юпитера, в том числе:

       – рассмотрены варианты выведения КА на орбиту Европы с использованием гравитационных маневров у Ио, Европы и Ганимеда;

       – построены графики зависимости затрат характеристической скорости от высоты первого импульса торможения и от периода начальной орбиты спутника Юпитера.

       3) Получены массовые характеристики КА для различных типов носителей.

       По результатам исследований был сделан доклад на семинаре по проекту «Лаплас» 30-го сентября 2008 г.

       Результаты работы: доклад, рабочие материалы.

 

       2. Астероид (99942) Апофис: анализ астероидной опасности (научный руководитель Р.Р. Назиров).

       В рамках работ по оценке опасности падения на Землю астероида Апофис были проведены следующие исследования:

       1) Проведен анализ существующих оптических и радиолокационных измерений орбиты астероида. На основе этого анализа получены характеристики будущих измерений.

       2) Создана программа на компьютере и с ее помощью подготовлены исходные данные для оценки точности определения орбиты астероида по разным составам измерений (такие оценки были получены Б.Ц. Бахшияном и К.С. Федяевым).

       3) Найдены несколько оптимальных траекторий полета к астероиду Апофис в 2011–2022 гг. с целью установки в окрестности астероида радиомаяка для проведения более точных измерений орбиты астероида.

       По результатам исследований был представлен совместный с Б.Ц. Бахшияном и К.С. Федяевым доклад на семинаре, посвященном астероиду Апофис, 31 октября 2008 г.

       Результаты работы: материалы доклада, результаты расчетов, рабочие материалы.

 

с.н.с.,  к.ф.-м.н.  А. А. Суханов, sukhanov@iki.rssi.ru

 

 

11. Модификация программного обеспечения для оптимизации межпланетных перелетов с большой и с малой тягой. Разработка математических методов и создание программного обеспечения для нахождения оптимальных межорбитальных перелетов с малой тягой по многовитковым спиральным траекториям вблизи планет.

 

Был существенно модифицирован комплекс программ оптимизации перелетов с большой тягой с возможностью облета нескольких небесных тел. Результатом модификации явилось следующее:

       1) В программах Voyage (нахождение оптимальных траекторий перелета) и Animation (анимация движения планет и КА) добавлена возможность нахождения оптимальных активных маневров в дальнем космосе (т.е. на траектории перелета между двумя телами или заданными положениями). Это дало возможность анализа значительно более сложного маневрирования в космосе.

       2) Меню ввода исходных данных было сделано более удобным.

       3) Программа ApproachAst (поиск астероидов вблизи найденной оптимальной траектории перелета) была переведена в графический режим с изображением траектории перелета и найденных астероидов; это сделало поиск астероидов более простым и наглядным.

       4) Прежняя база данных планетных орбит DE200 была заменена на более точные и совершенные базы DE405, DE414, DE421.

       5) Была создана новая база орбитальных данных астероидов, насчитывающая более 192 тыс. орбит нумерованных астероидов.

       Были также модифицированы и добавлены отдельные подпрограммы и функции, что повысило возможности комплекса.

       Результаты работы: программы на языке фортран, базы данных, результаты расчетов.

 

с.н.с.,  к.ф.-м.н.  А. А. Суханов, sukhanov@iki.rssi.ru

 

12. Перспективные методы формирования управления подвижными объектами

 

Бахшиян Б. Ц., Горяинов А. В. Скелетный алгоритм решения задач линейного программирования и его применение для решения оптимальных задач оценивания. // Вестник Московского авиационного института, 2008, том 15, № 2, С.5 - 16.

            Разработан новый алгоритм решения обычных и многопараметрических (обобщенных) задач линейного программирования, гарантирующий отсутствие почти вырожденных итераций и не требующий операций обращения матриц. Алгоритм опробован на оптимальных задачах  минимаксного оценивания для полиномиальной и тригонометрической моделей.


Бахшиян Б.Ц., Войсковский М.И. О множестве оценок наименьших модулей при линейных ограничениях. Известия РАН. Теория систем и управления. 2009.

            Рассматривается вопрос о неоднозначности оценки наименьших модулей при
линейных ограничениях на оцениваемые параметры. Предлагается эффективный
алгоритм нахождения множества оценок и выбора подходящей точечной оценки.
Приводятся результаты численных экспериментов.

 

Сиротин А.Н. «О некоторых геометрических свойствах  экстремалей в задаче оптимальной переориентации сферически симметричного твердого тела» принята в печать в 2008 году в «Известия РАН. Механика твердого тела».

             Исследуется задача оптимального управления пространственной переориентацией вращающегося твердого тела с единичным тензором инерции. Установлены новые геометрические свойства экстремалей данной вариационной задачи для невырожденного случая. Подробно описан эффект «схлопывания» экстремалей и его связь с плоским разворотом. Показано, что для каждой экстремали справедливы некоторые ранговые свойства. Полученные результаты основаны на анализе системы уравнений, получаемой в результате применения формализма принципа максимума Понтрягина, и использовании первых интегралов. Задача оптимальной переориентации тела со сферической симметрией (простейший вариант общей задачи) до сих пор не имеет полного решения, и поэтому представляют интерес новые факты, проливающие свет на неизвестные ранее.

 

A.I. Matasov. Correct filtering algorithms for stochastic delay differential equations.

Proceedings of the Leverhulme International meeting on stochastic delay differential equations.

Invited Lectures. Chester, UK, November, 2008. CD-ROM.

 

            Задача фильтрации в системах с запаздыванием является нетривиальной проблемой, так как алгоритмы ее решения содержат сложную нелинейную систему функционально-дифференциальных уравнений. В работе предложены и исследованы конструктивные алгоритмы решения задачи фильтрации в динамических системах с запаздыванием. При этом с помощью теории двойственности выпуклых вариационных задач построена оценка уровней неоптимальности для приближенных, но конструктивных алгоритмов фильтрации.

 

д.ф.-м.н. Бахшиян Б.Ц. bbakhshiyan@gmail.com

 

13. Разработка математической модели описывающей поведение локально однородных континуальных сильно охлажденных систем под воздействием энергии тектонических преобразований (применительно к Европе).

 

Разработано первое приближение математической модели описывающей поведение локально однородных сильно охлажденных систем. При аппроксимации механических свойств ледяных структур на поверхности Европы, использовались данные по механическим свойствам воды с учетом тепловых параметров, полученные в соответствии с теорией экстремальных свойств минимальных монокристаллов. Рассматривался процесс возможного дефектообразования в ледяных структурах за счет воздействия энергии тектонических преобразований. В работе использованы приемы математического моделирования ранее применяемые для анализа и прогнозирования течения металла при обработке металлов давлением.

 

Опубликованы статьи:

1. Чумаченко Е.Н., Назиров Р.Р. О некоторых проблемных вопросах, связанных с образованием хаотически расположенных особенностей рельефа на поверхности Европы// Известия РАН. Космические исследования, 2008, том 46, №5, с. 1-7.

2. Чумаченко Е.Н. Моделирование и оптимизация формоизменения пространственных сечений оболочек при сверхпластической формовке// Известия РАН. Механика твердого тела, 2008, №4, с. 143-153.

3. E. N. Chumachenko and R. R. Nazirov  Some Problems Connected with Formation of Chaotically Located Relief Peculiarities on Europa’s Surface // ISSN 0010-9525, Cosmic Research, 2008, Vol. 46, No. 6, pp. 499–505. © Pleiades Publishing, Ltd., 2008.

 

 д.т.н. Чумаченко Е.Н. mmkaf@miem.edu.ru

 

 

14. Математическое моделирование взаимодействия объектов с большой разницей температур. Построение модели для оценки эффективности криоботов.

 

Осуществлена постановка задачи математического моделирования взаимодействия объектов с большой разницей температур. Показано, что в первом приближении целесообразно использование твердотельного представления при описании механических свойств воды в широком диапазоне пониженных температур. Построена базовая модель для оценки эффективности криоботов.

 

В сборнике трудов опубликованы материалы по научному докладу:

Е.Н.Чумаченко, Р.Р.Назиров, И.В.Логашина Математическая модель перемещения криобота // Сб. трудов V-й МНПК «Исследование, разработка и применение высоких технологий в промышленности» / СПб., 2008. – Том 12 – с.132-133.

 

д.т.н. Чумаченко Е.Н. mmkaf@miem.edu.ru

 

15. Исследование имитационной математической модели и анализ гипотез по системам «протаивания» сплошной среды при низких температурах. Построение начальных оценок эффективности криоботов на Европе.

 

Выполнено исследование имитационной математической модели (в первом приближении) и анализ гипотез по системам «протаивания» сплошной среды при низких температурах. Анализ начальных оценок эффективности криоботов позволил предположить целесообразность их использования на Европе. Намечен новый комплекс исследований. Полученные результаты были опубликованы на международной конференции в Санкт Петербурге (см. п. 5.1.14.)

к.т.н. Логашина И.В. mrsirene@rambler.ru

 

 

16. Выполнение расчетов и анализ процессов образованию выступов, линз, лунок и трещин на поверхности Европы.

 

Выполнен комплекс расчетов по математической модели, описывающей процессы образования выступов, линз, лунок и трещин на поверхности Европы. Полученные материалы были использованы при анализе вышеназванных процессов и затем систематизированы в публикациях (см. п. 5.1.13.)

Ишутин П.Г.

 

17. Исследование способов построения транспортной системы Земля-Луна с использованием вращающихся тросовых систем, движущихся по орбитам около Земли и Луны. Оценка возможности создания транспортной трассы между Землей и Марсом  с использованием тросовых систем.

 

Одним из способов построения транспортной системы Земля – Луна является постановка на орбитах искусственных спутников трех пращей: двух из них на околоземных орбитах и одной – на окололунной.

            Найдены параметры околоземных и окололунной орбит, а также скорости грузов  на околоземных орбитах и направления их движения на этих орбитах.

            Ближайшая к Земле орбита имеет малый эксцентриситет и после отцепления от нее транспортируемого груза становится почти круговой. Груз, получивший дополнительную энергию, стыкуется со второй пращей, находящейся на высокоапогейной орбите с большим эксцентриситетом. Вторая праща позволяет грузу после отцепления долететь до Луны. Далее должен осуществляться контакт между транспортируемым грузом и лунной пращей.

            Аналогичный подход позволяет решить и проблему транспортировки грузов с Земли на Марс. При этом дополнительная скорость по сравнению с предыдущей задачей не превышает 0.5км/с.

д.т.н. Сидоров И.М., тел.333-14-89

 

18. Разработка способов прецизионного сближения и стыковки обменных грузов между вращающимися тросовыми системами, двигающимися по разным орбитам.

 

Для передачи транспортируемого груза с одной вращающейся пращи на другую необходим новый способ стыковки, кардинально отличающийся от традиционного.

            Момент отделения груза от пращи и параметры дальнего сближения определяются с помощью спутниковой системы глобального позиционирования. Вычисляется номинальная траектория перелета. При выполнении перелета ввиду неизбежных ошибок измерительных систем и исполнительных органов траектория движения груза отклоняется от номинальной. Предполагается, что коррекция движения выполняется корректирующими ракетными двигателями, установленными на передаваемом грузе. На конечном этапе решается задача стыковки.

            Подробно рассмотрена новая схема стыковки с автоматическим управлением процессом сближения и посадки, работающая с использованием алгоритма с «моделью» и решением краевой задачи. В настоящий момент готовятся к публикации 2 препринта.

 

д.т.н. Сидоров И.М., тел.333-14-89

 

Грант РФФИ 05-08-17894 (руководитель В.И Прохоренко)

Завершена работа по гранту РФФИ «Разработка принципов проектирования орбит и систем ориентации и стабилизации ИСЗ и КА нового поколения, обеспечивающих длительное функционирование этих объектов».  Полный отчет будет направлен в РФФИ  до 15 января 2009.

 

При частичной поддержке гранта  за весь период  2005-2008 были подготовлены следующие публикации:

1.     Рабинович Б.И., Прохоренко В.И. О гидродинамической аналогии решения двукратно осредненной проблемы Хилла // Космич. исслед. 2005. Т. 43. № 2. С. 126 – 134.

2.     Рабинович Б.И., Прохоренко В.И. О гидродинамической аналогии решения двукратно осредненной проблемы Хилла, возмущенного прецессией плоскости орбиты возмущающего тела // Космич. исслед. 2005. Т. 43. № 5. С. 378– 385.

3.     Рабинович Б.И., Мытарев А.И. Об устойчивости вращающегося космического аппарата, частично заполненного жидкостью. Случай одной полости // Космич. исслед. 2006. Т. 44. №  3. С. 239 – 248.

4.     Рабинович Б.И., Мытарев А.И. Об устойчивости вращающегося космического аппарата, частично заполненного жидкостью. Случай нескольких полостей // Космич. исслед. 2006. Т. 44. № 5. С. 452 – 458.

5.     Рабинович Б.И. Неустойчивость жидкостных ракет и космических аппаратов и некоторые фрагменты истории борьбы с ней // Полет, 2006. № 10. С. 18 – 26.

6.     Назиров Р.Р., Рабинович Б.И., Мытарев А.И., Докучаев Л.В. МГД-элемент в задачах ориентации и стабилизации вращающихся космических аппаратов // Полет, 2006. № 11. С. 21 – 28.

7.     Прохоренко В.И. Долговременная эволюция орбит ИСЗ под влиянием гравитационных возмущений, обусловленных сжатием Земли, с учетом возмущений от внешних тел // Изв. Вузов. Физика. Издание ТГУ. 2006. №2. Приложение. С. 63-73.

8.     Прохоренко В.И. Параметрическое исследование проблемы соударения спутника с центральным телом конечного радиуса в рамках ограниченной проблемы трех тел в Хилловском приближении. Фундаментальные и прикладные проблемы современной механики (Материалы V Всероссийской научной конференции). Томск, 3 – 5 окт. 2006 г. Т.: Изд. Томского государственного университета. 2006. С. 452 – 453.

9.     Прохоренко В.И. Об условиях пересечения орбиты спутника с поверхностью центрального тела конечного радиуса в двукратно осредненной ограниченной задаче трех тел // Труды МИАН РАН , 2007.  Т. 259. С. 156-173.

10.  Назиров Р.Р., Рабинович Б.И., Мытарев А.И. О применении        магнитогидродинамического элемента в контуре управления вращающимся космическим аппаратом  с полостями, частично заполненными жидкостью // Космич. исслед. // Космич. исслед. 2008. Т. 46. №  3. С. 256– 269.

11.  Назиров Р.Р., Рабинович Б.И., Мытарев А.И. О применении        магнитогидродинамического элемента в контуре управления вращающимся космическим аппаратом  со штыревой антенной // Космич. исслед. Принято в печать.

12.  Рабинович Б.И.  О возможности создания ракетно-магнитогидродинамического двигателя // Сб. Космонавтика и ракетостроение, 2008. № 4.

13.  Прохоренко В.И. Планетоцентрическая гравитационная сфера доминирующего влияния возмущений  от сжатия планеты над  возмущениями от внешних тел // Космич. Исслед.  Принято в печать.

14.  V. Prokhorenko. Gravitational Sphere of Dominant Perturbations Caused by Planetary Oblatness in Comparison with Perturbations of the Third Body. Proceedings.  International astronomical  meeting “Dynamics of Solar System Bodies” , Tomsk, July 27 –   August 1, 2008.

 

Работы, выполненные вне плана:

 

1. Баллистическое обеспечение эксперимента Плазма–Ф на Космическом аппарате Спектр-Р (Радиоастрон). По заказу отд. 54. Представитель заказчика Г.Н. Застенкер  

 

Предварительные расчеты предлагаемых вариантов орбиты для прогноза эволюции орбиты,  времени баллистического существования КА, навигационных параметров вдоль орбиты и времени прохождения различных областей магнитосферы.                          

Исполнители: Беляева Н.П., Прохоренко В. И.   

 

2. Навигационное обеспечение послеполетной обработка информации проекта Интербол.

По заказу отд. 54. Представитель заказчика Г.А. Котова. 

 

Модификация программного обеспечения и расчет дополнительных геофизических параметров вдоль орбит Аврорального и Хвостового зондов проекта Интербол.

 Исполнители: Беляева Н.П., Прохоренко В. И.   

 

с.н.с. к.ф.-м.н.  В. И. Прохоренко, тел.  333-50-45,   vprokhor@iki.rssi.ru