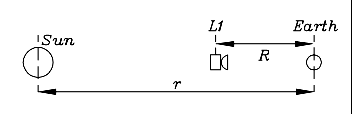
En s'aidant des sections (20) et (21), des mathématiques avec approximations de (M-5) et en postulant que les orbites sont toutes des cercles, il est assez facile de calculer la distance au point de Lagrange L1 (ou L2).
Nous commençons en reprenant le calcul de la 3ème loi de Kepler pour les orbites circulaires.
Et multipliant les deux côtés par r/m
Si T est la période de l'orbite, et étant donné que la distance parcourue par la Terre pour une orbite est 2 π r,
D'ou on tire la 3ème loi de Kepler pour des orbites circulaires (en multipliant simplement les deux côtés par r3T2). Considérons ensuite un vaisseau spatial de masse msc , placé sur la ligne reliant la Terre au Soleil, à une distance R de la Terre et (r-R) du Soleil (dessin).La force F d'attraction vers le Soleil est diminuée de celle de la Terre, en direction opposée, aussi :
Supposons que ce vaisseau spatial se déplace, comme la terre, en cercle autour du Soleil, avec une vitesse vsc . Alors si la force centrifuge équilibre l'attraction (ou bien, l'attraction fournit la force centripète)
Comme pour le calcul précédent, l'ensemble est multiplié par (r-R)/msc , ce qui donne
Supposons que ce vaisseau spatial se déplace également en cercle autour du Soleil, avec un rayon (r-R). (Ce qui, bien sur, implique que la Terre soit toujours positionnée dans la direction opposée du Soleil, un sujet sur lequel nous reviendrons bientôt). La période orbitale Ts c du satellite est alors, comme auparavant
Ou, en divisant le tout par (r-R)2
Ce qui revient à la précédente équation de la " 3ème loi", sauf que l'on a tenu compte de l'attraction opposée de la Terre, qui est maintenant ajoutée. Mais la Terre sera-t-elle toujours placée au point où sa traction sur le satellite est exactement face du Soleil ? Non, à moins moins que les deux périodes orbitales ne soient les mêmes :
Alors seulement le déplacement du vaisseau spatial correspond à celui de la Terre et leur distance reste constante. Ce qui n'arrive en principe que pour une valeur de R, bien définie par rapport à la Terre. Cette distance,R, est désormais le nombre inconnu que nous devons rechercher, c' est "la chose" que nous recherchons. Si Tsc = T, les deux relations comportant 4 π2/T2 du côté droit sont égales, fournissant ainsi une équation dont on peut calculer R. Cette équation est
Divisons les deux côtés par GM: G est alors éliminé, et à la place des masses (m,M) (de la Terre, du Soleil) nous n'avons plus que leur proportion, un petit nombre que nous nommerons y
ou en notation scientifique (le point signifiant multiplication)
L'équation devient : Multiplions chaque côté par r3 Ce qui permet de continuer à simplifier en prenant le rapport de r à R. : z = R/r, qui est lui aussi un petit nombre, puisque le vaisseau spatial est toujours beaucoup plus proche de la Terre que du Soleil. Pour l'obtenir, on a multiplié les deux côtés, haut et bas, par r3 [C' est le même si on multiplie par (1/ r3)/(1/r3). Cela revient à multiplier par 1, mais permet de faire apparaître une nouvelle variable z équivalente à R/r . Le résultat est :
Maintenant nous sommes prêts "à rouler", à trouver la quantité inconnue z. L'équation ci dessus est compliquée. En fait il n'existe probablement pas de formule exacte pour sa solution. Cependant, puisque z est petit, il est assez facile d'obtenir une solution approximative, en employant les méthodes de la section (M-5), ou il a été montré que :
La substitution dans l'équation principale par ces approximations équivalentes donne
Les côtés de l'équation sont tous deux maintenant également petits. Le côté droit n'est seulement légèrement augmenté que de z : nous pouvons laisser tomber ce terme sans faire beaucoup de différence. Alors
Ainsi la distance à L1 est à environ 0.01 de la distance au Soleil. Il devient possible de revenir aux équations plus exactes, comme 3z3 ~ y(1+z), et de remplacer z à droite par sa valeur approximative 0.01, pour obtenir des solutions plus précises. Un tel processus d'amélioration graduelle, appelé itération, est aussi utilisé avec l'équation de Kepler, discutée dans la section (12a). à cause de la petitesse de z, ces modifications ne font que très peu de différence. Le calcul de la distance du point L2, ( côté nuit ) de Lagrange est tout à fait analogue (comme d'ailleurs son résultat). Dans ce cas les équations impliquent r+R à la place de r-R, et dans l'équation de F les termes sont ajoutés au lieu de soustrait, parce que maintenant le Soleil et l'attraction de la terre sont dans la même direction. Essayez ! |