Site Map

(M-11)  Deriving   sin(a+b),   cos(a+b)

    Take Note!   The illustration below uses the Greek letters ""alpha" and "beta", written as a and b. If all you see here are the letters "a" and "b", your browser is overriding the font specification, and everywhere below (in the title above, too), these letters appear as "a" and "b."

Given the functions (sina, cosa, sinb and cos b), we seek formulas that express sin(a+b) and cos(a+b). The first of these formulas is used in deriving the L4 and L5 Lagrangian points, here.

Please verify every calculation step before proceeding!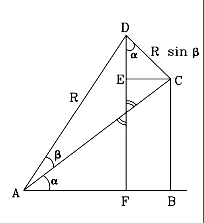

As shown in the drawing, to derive the formula we combine two right-angled triangles

    ABC which has an angle a
    ACD which  "   "    "  b
The long side ("hypotenuse') of ACD is AD=R. Therefore

    DC = R sin b
    AC = R cos b
Similarly

    BC = AC sin a = R cos b sin a
    AB = AC cos a = R cos b cos a
The triangle ADF is right-angled and has the angle (a+b). Therefore

    R sin (a+b) = DF
    R cos (a+b) = AF

Start by deriving the sine:

    R sin (a+b) = DF  =  EF + DE  =  BC + DE
  Note in the drawing the two head-to-head angles marked with double lines: like all such angles, they must be equal. Each of them is one of the two sharp ("acute") angles in its own right-angled triangle. Since the sharp angles in such a triangle add up to 90 degrees, the other two sharp angles must be equal. This justifies marking the angle near D as a, as drawn in the figure.

In the right-angled triangle CED

    DE = DC cos a = R sin b cos a
    EC = DC sin a = R sin b sin a
Earlier it was already shown that
    BC = R cos b sin a
    AB = R cos b cos a
Therefore

 R sin (a+b)  =  BC+DE  =  R cos b sin a + R sin b cos a

Cancelling R and rearranging a to precede b

   sin (a+b)  =  cos b sin a + sin b cos a

Similarly, for the cosine

R cos (a+b) = AF = AB - FB = AB - EC =

        = R cos b cos a - R sin b sin a

Cancelling R and rearranging

   cos (a+b)  =  cos a cos b - sin a sin b

Application of these formulas:  #34b  The L4 and L5 Lagrangian Points

Trigonometry Proficiency Drill

More "Trig": The Tangent

Author and Curator:   Dr. David P. Stern
     Mail to Dr.Stern:   audavstern("at" symbol)erols.com .

Last updated 25 November 2001