| En ausencia de fuerzas, el movimiento en línea recta y a velocidad
constante continúa indefinidamente. El movimiento circular, sin
embargo, necesita fuerzas para existir.
Imagine que tiene una piedra amarrada a una cuerda y está moviéndola en círculos de radio R (metros). Cada rotación la piedra cubre una distancia de 2pR metros donde p = 3.14159265359. . . es la razón entre el diámetro del círculo y su circunferencia. Figúrese además que la piedra efectúa N círculos ("revoluciones") por segundo. Como su velocidad v es igual a la distancia que se mueve en un segundo, vemos que v = 2pNR m/s 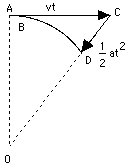
Si tomamos el movimiento desarrollado en un momento muy breve, el trayecto AB cubierto es tan pequeño que su curvatura se puede desechar, permitiendo ver el movimiento como si fuese en línea recta, con una velocidad v. Después de un rato, no obstante, la diferencia entre este movimiento y una línea recta se hace evidente: el movimiento recto con velocidad v llevará a la partícula al punto C, a la distancia de AC = vt mientras que el movimiento real la lleva al punto D en un círculo, cuyo centro se indica por O. Es útil estimar este movimiento como la suma de dos movimientos separados: un movimiento en línea recta de A a C, y un movimiento adicional de C a D que devuelve a la partícula al círculo. Como se indicó anteriormente (en la sección sobre vectores ), cuando un movimiento es una combinación de dos movimientos simples, el desplazamiento resultante se puede obtener deduciendo de forma separada los desplazamientos producidos por cada movimiento aislado, y luego sumándolos conjuntamente. Es movimiento resultante de la suma desde C a D es el que interesa aquí. Su dirección es siempre hacia el centro, y la distancia CD cubierta por el, indicada aquí por x, puede obtenerse del teorema de Pitágoras, aplicado al triángulo OAC (el cálculo se asemeja al que obtenía la distancia al horizonte en la sección (8a)). En ese triángulo, OA = R, AC = vt, OC = R + x. Por lo tanto R2 + v2t2 = (R + x)2 = R2+ 2Rx + x2 Restar R2 de ambos lados v2t2 = 2Rx + x2 = x(2R + x) Si el intervalo de tiempo t es muy pequeño, x es mucho más pequeño que 2R y puede desecharse por equiparación. Luego v2t2 = 2xR Pero debido a una fórmula anterior, en la sección sobre la aceleración, esta es exactamente la distancia cubierta en el tiempo t por un movimiento con aceleración a = v2/R El resultado anterior nos sugiere que el movimiento constante alrededor de un círculo, al menos durante un pequeño intervalo, se puede ver como la suma de un movimiento en línea recta con una velocidad fija v, más un movimiento acelerado hacia el centro de atracción, con la antedicha aceleración a. La conclusión es correcta, aún cuando la deducción es algo irregular. La deducción convencional (como la mayoría de la teoría de los movimientos) requiere el uso del cálculo diferencial, el estudio de cantidades cambiantes y de la forma como cambian, así como también estar familiarizado con los vectores. Aceleración centrípeta y fuerza centrípetaLa aceleración a = v2/R hacia el centro, que se necesita para mantener un objeto moviéndose en un círculo, se llama su aceleración centrípeta, del Latín petere, moverse hacia. Por las leyes de Newton, cualquier aceleración requiere una fuerza. Si una piedra (o cualquier otro objeto) de masa m gira con velocidad v alrededor de un eje central O, a la distancia R desde él, una fuerza F debe tirar constantemente de él hacia el centro yF = ma = mv2/R Este es conocida como la fuerza centrípeta que, tirando
continuamente de la piedra, mantiene la cuerda estirada. Si la cuerda se
rompiera, por ejemplo, por el punto A del dibujo, la piedra continuará
con velocidad v en línea recta a lo largo de AC. Y no volará
hacia fuera a lo largo de OA, como algunos creen, ¡aún cuando
esa sea la dirección en la que está estirada la cuerda!
|