 (Extensión
Opcional)
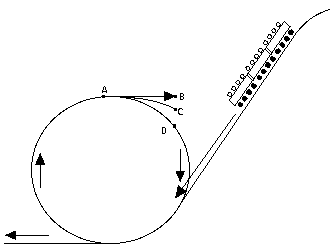
En la sección precedente el movimiento de la montaña rusa "looping" se trató usando la fuerza centrífuga. También puede verse este problema desde el punto de vista del mundo exterior, usando la fuerza centrípeta, pero no es fácil. En el punto A, en lo alto del bucle, ambas fuerzas, la de gravedad y la centrípeta, apuntan hacia abajo. Luego, ¿qué es lo que mantiene a los pasajeros en sus asientos? Déjenme resolver ese movimiento usando el concepto de fuerza centrípeta. Un vagón que va alrededor de un bucle, de radio R y velocidad V, se acelera a razón de V2/R hacia el centro (con tal de que se mantenga sobre los railes) y por consiguiente está sujeto a la fuerza centrípeta V2/R, también dirigida hacia el centro. Cuando el vagón está en el punto A, esta fuerza apunta hacia abajo. Tomando "abajo" como la dirección positiva a lo largo del eje vertical. |