Usando las herramientas de las secciones (20) y (21), las matemáticas
de soluciones aproximadas desarrolladas en (M-5), y asumiendo que todas
las órbitas son círculos, es relativamente sencillo calcular
la distancia al punto Lagrangiano L1 (o al L2). Comenzamos repitiendo la
derivación de la 3ª Ley de Kepler para órbitas circulares.
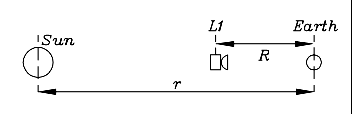 Denominemos G a la constante gravitacional, M a la masa del Sol, m a la de la Tierra, r a la distancia entre la Tierra y el Sol y v a la velocidad en su órbita. Aplicando lo sabido sobre fuerzas centrífugas y centrípetas, obtendremos (como en la sección (20)) GMm/r2 = mv2/r y multiplicando ambos lados de la igualdad por r/m GM/r = v2 Si T es el período orbital, y como la distancia cubierta por la Tierra en cada órbita es 2πr, vT = 2π r Dividido por T Elevando al cuadrado: y sustituyendo Dividimos ambos lados por r2: GM/ r3 = 4π2/T2 de lo cual deducimos la 3ª ley de Kepler para órbitas circulares (solamente multiplicando ambos lados por r3T2). Considere ahora a msc la masa de un vehículo espacial localizado en la línea que conecta la Tierra y el Sol, situado entre los dos, a una distancia R de la Tierra y a una (r-R) del Sol (dibujo). La fuerza F que lo atrae hacia el Sol está contrarrestada por la atracción de la Tierra en la dirección opuesta, así que F = GMmsc /(r-R)2 – Gmmsc /R2 Dado que este vehículo también se mueve en un círculo alrededor del Sol, con una velocidad vsc . Entonces, si la fuerza centrífuga equilibra la atracción (o de otra manera, la atracción suple a la fuerza centrípeta) GMmsc /(r-R)2 – Gmmsc /R2 = msc vsc 2/(r-R) De forma similar al cálculo anterior, se multiplican ambos lados por (r-R)/msc , dando GM/(r-R) – Gm(r-R)/R2 = (vsc )2 También asumimos que el vehículo se mueve en un círculo alrededor del Sol, de radio (r-R). (Por supuesto que esto requiere que la Tierra esté siempre en su sitio para atraerlo en la dirección opuesta a la del Sol, un asunto que trataremos pronto). El período orbital Tsc del satélite satisface, como antes vsc Tsc = 2π(r-R) de donde Luego obtendremos GM/(r-R) – Gm(r-R)/R2 = 4π2(r-R)2/(Tsc )2 dividiendo todo por (r-R)2 GM/(r-R)3 – Gm/R2(r-R) = 4π2/(Tsc )2 que se asemeja a la anterior ecuación de la "3ª ley", excepto que ahora está añadida la atracción opuesta de la Tierra. Pero, ¿estará siempre la tierra ubicada donde su atracción sobre el satélite sea exactamente la opuesta a la del Sol?. No, a menos que los dos períodos orbitales sean iguales: Tsc = T Solo entonces el movimiento del vehículo se empareja con el de la Tierra y la distancia entre ambos permanece constante. Esto solo ocurre, en general, para un valor de R, esto es, solo a una distancia desde la Tierra, y esa distancia, R, es el número desconocido que necesitamos deducir, el "objeto" que estamos buscando. Si Tsc = T, las dos relaciones con 4π2/T2 en la parte derecha son iguales entre si, esto nos proporciona una ecuación a partir de la que podemos deducir R . Esa ecuación es GM/(r-R)3 – Gm/R2(r-R) = GM/r3 Si dividimos ambos lados por GM: G desaparece de la escena, y en lugar de las masas (m,M) del Sol y la Tierra, tenemos solo su relación, un número pequeño que denominaremos y y = m/M = 3/1,000,000 o en notación científica y = m/M = 3/106 (ó 3.10-6) La ecuación es ahora Puede aún simplificarse más. En lugar de trabajar con r y R, déjenme introducir su relación z = R/r, que es también un número pequeño, dado que el vehículo está siempre más cerca de la Tierra que del Sol. Para hacer eso, multiplique ambos lados por r3, que se puede también conseguir dividiendo por r3 los denominadores de ambos lados. El resultado: 1/(1-z)3 – y/z2(1-z) = 1 Ahora estamos listos para deducir la cantidad desconocida z. La fórmula superior es complicada, de hecho, probablemente no existe una fórmula exacta para su solución. No obstante, como z es pequeño, es más bien fácil obtener una solución aproximada usando los métodos de la sección (M-5). Allí fueron mostrados como 1/(1-z)3 ~ 1 + 3z Substituyendo estas aproximaciones en la ecuación principal nos da 1 + 3z – [y/z2] (1+z) ~ 1 Ambos lados son ahora igual de pequeños. El lado de la derecha está ligeramente modificado con la suma de z: podemos prescindir de este término sin obtener una gran diferencia. Luego 3z3 ~ y = 3/1,000,000 z3 ~ 1/1,000,000 Calculando la raíz cúbica R/r = z ~ 1/100 = 0.01 Luego, la distancia a L1 es aproximadamente 0.01 de la distancia al Sol. Ahora es posible regresar hacia ecuaciones más exactas, como 3z3 ~ y(1+z), y reemplazar la z de la derecha por su valor aproximado de 0.01, para obtener unas soluciones más precisas mediante un proceso de progresión gradual, llamado iteración, también usado con la ecuación de Kepler planteada en la sección (12a). Debido a la pequeñez de z, con las modificaciones hechas aquí se obtiene poca diferencia. El cálculo de la distancia del punto L2 en el lado
oscuro es muy similar, así como su resultado. En este caso las ecuaciones
conciernen a r+R más que a r-R, y en la ecuación
de F los términos son sumados en vez de restados, porque
ahora el Sol y la Tierra ejercen la atracción en la misma dirección.
¡Compruébelo!
|