#21c     Vuelo a Marte: Cálculos

Notación y velocidades de escape

    Antes de comenzar, ayudará establecer una notación para las cantidades usadas aquí. Aún cuand algunas de ellas son vectores, solamente sus magnitudes serán utilizadas. Negrita es solamente utilizada para acentuar, nunca para indicar el carácter del vector.

    Como antes, r₁ = 1 AU es la distancia de la Tierra desde el Sol, r₂ = 1.523691 AU la de Marte, y (como aproximación) se asume que ambos planetas se mueven en círculos.

    Velocidad V será medida en kilómetros por segundo (km/s), y diferentes velocidades son identificadas con subíndices. Minúscula v identifica velocidades asociadas con órbitas alrededor de la Tierra antes que alrededor del Sol.

    La sección anterior también introdujo la velocidad órbital V₀ de la tierra alrededor del Sol, alcanzando alrededor de 30 km/s (más precisamente, 29.77 km/s), mucho mayor que v₀ ~ 8 km/s (aprox.) requerida por un satélite para rodear la Tierra sobre su superficie (ignorando la atmósfera).En la sección #21 notamos que la velocidad de escape v_e desde una órbita tan baja es obtenida multiplicando v₀ por la raíz cuadrada de 2, igual a 1.41421356.... aproximada aquí en 1.414. Esto dá
   

    Tal astronave, sin embargo, aún no es libre de moverse a cualquier punto en el espacio. La velocidad v_e ha obtenido su libertad de la gravedad Terrestre, pero no libertad de la atracción del Sol, alrededor del cual continúa moviéndose en una órbita similar a la de la Tierra, a V₀ =30 km/s .

    La situación ahora es completamente análoga a escapar de una órbita de baja altitud (solo que el costo es mayor!) Para liberarse de una órbita circular alrededor del sol y abandonar el sistema solar, la nave espacial necesita expandir su velocidad a una "segunda velocidad de escape".
   

    Para alcanzar V_e ésta debe de alguna manera incrementar su velocidad en 12.42 km/s adicionales--más de lo que se necesita para escapar de la gravedad de la Tierra, comenzando desde el resto de la superficie! Afortunadamente, existen maneras (tratadas en la Sección #35) de hacer que el movimiento de los planetas (o de la Luna) provean parte de este impulso.

    Otras velocidades que entran en el cálculo son la velocidad V₁ con la cual la nave espacial parte desde cerca de la Tierra y entra a la elipse de Hohmann (distancia r₁ desde el Sol), y la velocidad V₂ con la cual ésta alcanza la órbita de Marte (distancia r₂). Además, V₃ será la velocidad de Marte en su órbita, asumiendo que ésta tiene una magnitud constante (i.e asumiendo que la órbita de Marte es circular). Si V₂ > V₃, la nave espacial sobrepasa a Marte, mientras que con V₂ < V₃ ésta está siendo sobrepasada.

Ecuaciónes requeridas

    (1) Ley de Kepler

•     La Primera ley es "Los Planetas se mueven en elipses, con el Sol como centro" Esto ya está siendo usado, por ejemplo, la elipse de translado es una de esas órbitas.

•     La segunda ley es "La línea que conecta un planeta con el Sol recorre áreas iguales en tiempos iguales. " Permítanos extraer de esto una ecuación útil.

Aplicación de la 2da. Ley de Kepler

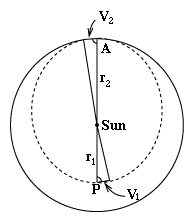
    El dibujo aquí muestra la órbita de Marte (sólida) y la elipse de translado (línea partida), con radios (r₁, r₂) a los puntos (perigeo, apogeo), en los cuales la velocidad de la nave espacial es (V₁, V₂). Los segmentos cortos dibujados en esas posiciones representan la distancia cubierta por la nave espacial en el siguiente segundo después de pasar perigeo o apogeo, y por la definición de velocidad ("distancia por segundo") ellos también igualan a V₁ y V₂. En realidad, esos segmentos deberían ser curvos como la órbita, pero siendo tan cortos, difieren en forma insignificante de las líneas rectas. Completamos entonces los triángulos largos y delgados, que tienen como base esas líneas.

    Note que cada uno de estos triángulos tiene un ángulo recto en la parte inferior, porque en el apogeo y perigeo (y en ningún otro lugar), la línea del Sol es perpendicular a la órbita.

    En el perigeo, la altura del triángulo es r₁, la longitud de su base es V₁, entonces por la ecuación para el área A₁ de un triángulo
   

    Cada uno de estos triángulos es barrido en un segundo, entonces, por la segunda ley de Kepler sus áreas pueden ser establecidas como iguales. Multiplicando amboslados de esa equivalencia por 2 productos
   

    La ecuación es numerada para ayudar a referirnos a ella mas tarde. Por favor note que la relación solamente de la órbita, el ángulo entre el radio y la órbita no es 900, y el área también depende de su exacto valor.

    La tercera ley de Kepler ya fué usada para determinar el periodo órbital. La necesitaremos nuevamente al final.

    (2) La Ecuación de La Energía

    En la sección #12 fué establecido que la energía E de un satélite de masa m órbitando la Tierra, en cualquier punto de su órbita, es

    Como notamos anteriormente, para que un objeto en la órbita terrestre escape completamente de la órbita del Sol (solo apenas!), necesita una velocidad V_e = 1.414..V₀ = 42.42 km/s. Sea E₀ la energía de tal objeto. Entonces si

    Debido a que éste tiene velocidad de escape, si esperamos un largo, largo tiempo, este objeto estará extremadamente lejos de la Tierra, y, habiendo agotado prácticamente toda su energía, su velocidad será muy cercana a cero. Entonces ambos términos del lado derecho de la ecuación (2) tienden a cero, sugiriendo
   

    Dividiendo por m y cambiando el término negativo V_e a la derecha

    por lo cual el valor de k podría ser escrito
   

Calculos

    Volviendo ahora a la nave espacial en la órbita de transferencia de Marte, su energía debería ser la misma en el perigeo P y en el apogeo A, entonces por la ecuación (2)

    Dividimos ambos lados por m ("cancela m") y multiplicamos ambos lados por 2

    Como primer paso, use la ecuación: (1) para expresar V₂ :

    Sustituyendo esto en el lado izquierdo de (4)

    Esto podría ser establecido como igual al lado derecho de (4), y luego tenemos ya una ecuación para el paso (2)--solo una ecuación, con solamente una incógnita , a saber V₁. Pero en lugar de apresurarse, es conveniente separar tantos factores como sea posible. Quizás algo se simplificará!

    Por una identidad bien conocida (vea también "Identidades")

entonces            

    Guarde la ec. (6) para referencia y considere seguidamente el lado derecho de (4). Podríamos introducir alli un común denominador r₂:

    Por (4), expresiones (6) y (7) son iguales:
   

    Nuestra premonición ha sido correcta: ambos lados pueden ser divididos por (r₂- r₁), eliminando ese término, y ambos lados pueden también ser multiplicados por r₂ , creando mas simplificaciones. Si nos hubiésemos apurado anteriormente, nuestras Expresiones podrían haber sido mucho mas tremendas! Lo que queda es
   

    Multiplique por r₂, divida por (r₂ + r₁), y la cantidad incógnita queda sola--al cuadrado, pero está bien:
   

    Es hora de incluir los números:
   

    Sacando raíces cuadradas de ambos lados (primera ley de álgebra)
   

mostrando que necesitamos adicionar solo 2.966 km/s, una pizca menos de 3 km/s ó 10% de la velocidad orbital.

Llegada a Marte

    Ha resignado una parte de su energía kinética para contrarrestar la atracción del Sol y moverse lejos del Sol. La gran pregunta ahora es --cómo se compara esto con la velocidad V₃ de Marte en su órbita?

    Para obtener velocidades en km/s, las distancias deben ser suministradas en kilómetros, y los tiempos en segundos, pero para "beneficio de los peatones", dividimos los cálculos, evitando números grandes y la notación científica. Comenzamos con la 3er. ley de Kepler para órbitas circulares, con distancia r en AU y periodo órbital T en años. Como surge de la sección precedente, (y también en la sección #10), en estas unidades

    Para Marte, r = 1.523691, T² = (1.523691)³ = 3.53745

Vayamos con el número aceptado 1.8822 (se hicieron algunas aproximaciones). Asumiendo 365.25 dias por año (Juliano):

    Durante ese tiempo la nave espacial cubre

    Dividiendo por T, esto llega a

Cada dia tiene (24)(3600) = 86400 segundos, entonces la distancia órbital cubierta por Marte cada segundo es

    Distancia por segundo es por supuesto la definición de velocidad. Por lo tanto

Vemos que Marte es el que se mueve mas rápido, y estára pasando a la nave espacial. Para igualar velocidades con Marte, la nave debe general un impulso extra de 2.545 km/s .