|
La elipse de transferencia de Hohmann se puede mostrar por ser medio más eficiente de empuje del cohete para alcanzar Marte. Otras trayectorias pueden llegar a allí más rápido, pero requerirán más empuje para empezar y un ajuste más grande del empuje al final, incluyendo quizás un cambio en la dirección. Algún inconveniente? Sólo uno: un requisito muy riguroso en las posiciones relativas de la Tierra y Marte en el tiempo del lanzamiento. Como se verá, las condiciones requeridas ocurren sólo una vez en aprox. 26 meses. Para volar de regreso desde Marte a la Tierra la elipse de Hohmann se puede utilizar también, pero igualmente, los planetas necesitan estar posicionados en el lugar exacto al tiempo del lanzamiento. Si los astronautas de la Tierra alguna vez llegan a la superficie de Marte, deben escoger entre esperar mas de un año para tener las condiciones correctas necesarias, o tomar un camino a casa más directo pero menos económico. A continuación se calcula esta demora. También se incluye el concepto del período sinódico de Marte, su período orbital como es visto desde la Tierra en órbita.
Las Orbitas de Hohmann - hacia y desde Marte
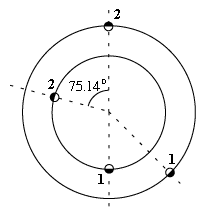
Los círculos utilizados la izquierda se utilizarán para marcar el movimiento de la Tierra (el círculo interior) y de Marte (el círculo exterior) alrededor de sus órbitas. Como se mostró en la sección #21b, cuando una nave espacial se lanza de la Tierra a Marte, ambos deben estar en los puntos indicados por "1." Después de 0.70873 años, la nave llega a Marte, que se ha movido mientras tanto al punto marcado como "2." ¿Dónde está la Tierra en ese momento? En un año, se mueve aprox 360 grados, así que en 0.70873 años se desplaza
ésta alcanzará por lo tanto la posición "2" en el círculo interior, 75.14 grados pasada la posición de Marte. Advierta cómo Tierra ha alcanzado Marte -- en el lanzamiento (posicion "1") quedó retrasada, pero ahora está adelantada. Como muestra la tercera ley de Kepler, cuanto más cerca está un planeta del Sol, más rápido completa su órbita, y la Tierra está más cerca que Marte. Suponga que la nave espacial que ha aterrizado en Marte es un robot, que toma una muestra e inmediatamente despega para su viaje del regreso. Lanzando desde el punto (2), después de liberarse de la gravedad de planeta, otra vez puede seguir la elipse de transferencia de Hohmann, en una imagen espejo del vuelo a Marte (dibujado abajo). Su viaje empieza con un empuje inverso de 2.545 km/s, reduciendo su velocidad orbital de V3 a V2. Entonces, después de 0.70873 años, llega otra vez al punto marcado (1) con la velocidad V1, la cual necesita ser reducida a la velocidad orbital de la Tierra V0 mediante un empuje inverso de 2.966 km/s. Desgraciadamente.. ¡La tierra no estará esperando allí! El Período Sinódico
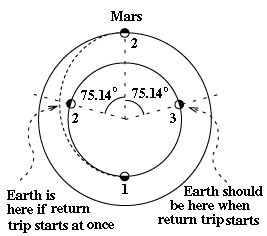
Veamos donde la Tierra debería estar al tiempo del lanzamiento desde Marte, para que el vuelo del regreso la encuentre en el momento apropiado. El viaje de regreso, siendo la mitad de la elipse de Hohmann, toma 0.70873 años, durante este tiempo (calculado arriba) la Tierra cubre un arco de 255.14 grados en su órbita. Para encontrar al cohete del regreso cuando alcanza la órbita de la Tierra en el punto (1), la Tierra debe estar -- en el comienzo del vuelo del regreso de Marte --255.14 grados detrás del punto "1" en su órbita. Eso la pone en posición (3), 75.14 grados detrás de la posición de Marte, no en la posición (2) donde Tierra está 75.14 grados adelante de Marte. Debido a que la Tierra y Marte cambian constantemente su posición relativa, es lógico que si demoramos suficientemente el viaje del regreso, la Tierra se moverá de la posición (2) relativa a Marte, a la posición (3), en ese momento el viaje de regreso puede empezar. Calculemos esa demora. Para simplificar el cálculo de la demora, nosotros calculamos la velocidad relativa de la rotación entre la Tierra y Marte alrededor del Sol.
Cada año, la Tierra se adelanta a Marte por (1 - 0.531293) = 0.468707 órbitas. En 2 años, el adelantamiento es (2) (0.468707) = 0.937414 órbitas y la Tierra estará una órbita completa adelantada después de
Si Marte y la Tierra comienzan uno al lado del otro, después de 2.13353 estarán otra vez parejos. Del punto de vista de un observador en la Tierra, eso es el tiempo requerido por Marte para un círculo completo alrededor del cielo. Es conocido como el período sinódico de Marte, y es aprox. de 25.6 meses. Lo demás es fácil. Para que Tierra cambie su posición relativa a Marte de (2) a (3), la Tierra debe avanzar (relativa a Marte) por Para avanzar 360 grados tarda 2.13353 años, así que avanzar por el encima del ángulo tarda
Un cálculo más exacto da 459 días (el nuestro contiene aproximaciones). Cuándo el cohete de regreso llega a la Tierra, éste estará sobrepasándola, ya que su velocidad V1 excede la velocidad orbital V0 de la Tierra por aprox. 3 km/s. Antes de desdender sin peligro, la nave espacial debe deshacerse también de la velocidad V0 dada por la atracción de la Tierra, aprox. 11.3 km/s. Sin embargo, si entra rozando la atmósfera, su energía cinética extra se disipará seguramente en forma de calor, sin necesidad de disparar mas cohetes. Reflexiones finalesNuestros esquemas sólo marcan el progreso en órbitas circulares alrededor del Sol, que mantienen aproximadamente la misma velocidad. El movimiento relativo de la Tierra y Marte en el cielo es mucho más variable, porque la distancia Tierra-Marte cambia todo el tiempo. En realidad, cuándo la Tierra está mas cerca de Marte y lo ha sobrepasado, Marte parecerá (por un tiempo) estar moviendose hacia atrás entre las estrellas. El período total sin embargo sigue siendo 25.6 meses, bastante diferente del período orbital verdadero de Marte que es 1.8822 años = 22.6 meses. Considerando todas esas complicaciones, uno puede apreciar la sutileza del trabajo de Copérnico y Kepler, quienes obtuvieron patrones nítidos y regulares del movimiento, partiendo de otros mucho menos regulares de los planetas de los cielos. |