| En un eclipse de Luna, si el ancho de la sombra de la Tierra
es el doble del ancho de la Luna, entonces la anchura de la Tierra es,
aproximadamente, tres veces la de la Luna y no dos como quizá se
pueda pensar. He aquí el porqué.
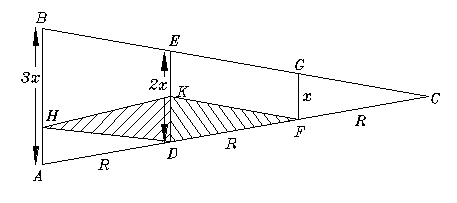
El Sol no es un punto de luz sino una fuente con gran extensión, con un disco cubriendo una parcela circular del cielo de unos 0.5º de ancho. Esto hace que la sombra de la Tierra no sea un cilindro extendiéndose hasta el infinito sin reducirse, sino un cono con un ángulo de 0.5º en su vértice C (vea el dibujo). Aquí AB es el diámetro de la Tierra y las direcciones AC y BC representan rayos desde los bordes opuestos del disco solar cuyas direcciones difieren 0.5º . |

| Si x es el diámetro de la Luna y R su distancia,
con arreglo a Aristarco, el ancho ED de la sombra a la distancia R
es igual a 2x (realmente, 2.5x es más cercano). Añadimos
al dibujo los puntos H y K, así que HA = KD = x.
El ancho de la Luna tal y como se ve desde el punto H es KD = x y como el tamaño de la Luna en el cielo es casi el mismo que el del Sol, el ángulo KHD (sombreado) será igual a 0.5°. Ahora prolongamos la línea AD = R una distancia R hasta el punto F. Los dos ángulos sombreados HKD y KFD son congruentes (= iguales en forma y tamaño) y tienen el mismo ángulo de 0.5º como el ángulo C. Efectivamente, ahora se puede probar que los triángulos GFC y AHD también son congruentes a los dos sombreados. Entonces resulta que AC = 3R y por proporciones simples (vea el dibujo) AB = 3x. |
|
Próxima Etapa: #9c Descubrimiento del Sistema Solar
Author and Curator: Dr. David P. Stern
Last updated 13 December 2001
|