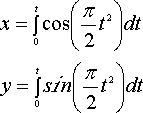|
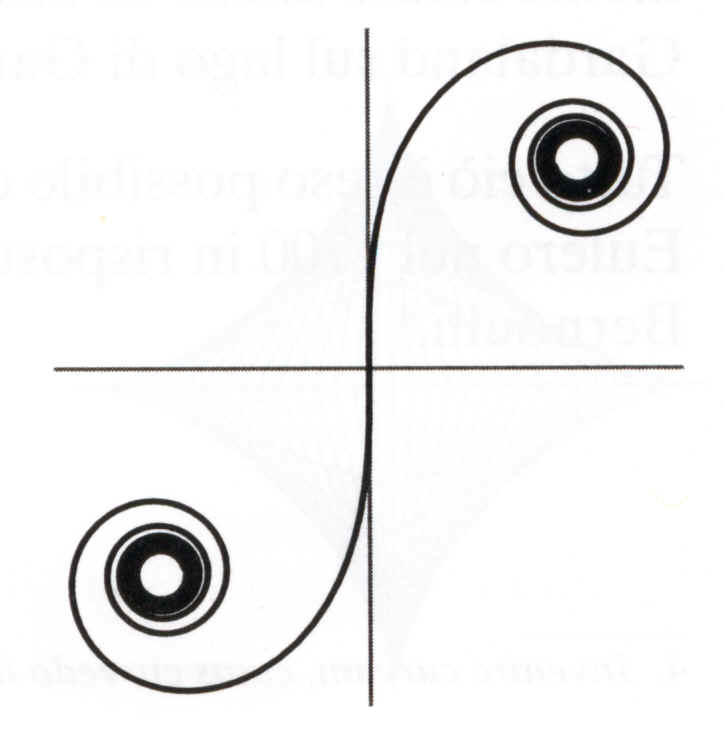
However, that curve had already been studied by Euler in 1700, in connection with a problem set by Jakob Bernouilli. Later on, it was used in 1800 by Marie-Alfred Cornu, Professor of Physics at the École Polytechnique of Paris, during his studies on light diffraction. By the end of the seventies it turned out that the clothoid curve was the ideal curve for looping rides in which people were turned upside down. Before that it was always believed that the logical shape for such a ride was a circle. Actually, if a roller coaster loops around a circle, the entrance to the loop has considerable curvature, imposing a strong centrifugal force on the passengers. On the other hand, when the car is reaching its highest point on the circle, its acceleration decreases in such a way that the passengers risk falling down headlong. Luckily we can use .......the clothoid, whose shape varies the acceleration to minimize the stress on riders. It brings them back safe and sound, to where their feet again stand on the ground.
This remarkable curve has a variable radius along its length. The force on the rider depends on two factors: the curvature of the track, and the speed of motion. Gravity slows down the ride as it rises higher, but at the same time the ride also speeds up where the track curves more sharply, because of the preservation of angular momentum. A similar effect occurs if you rotate a weight attached to a string: its rotation will slow down if you let out a greater length of string, and will speed up if the string shortens.
An arc of a clothoid has variable curvature, in every point proportional to the arc length (evaluated at the origin), and it provides the smoothest link between a straight line and a circular curve. It is used in roads and railroads design: the centifugal force actually varies in proportion to the time, at a constant rate, from zero value (along the straight line) to the maximum value (along the curve) and back again. The parametric equations of the clothoid are given by the so-called "Fresnel
Integrals":
The two spirals, symmetrical with respect to the axes origin, are characterized by their tendency toward two asymptotical points. This web page is an edited translation from a section of the Italian web site:
|