|
However, by Newton's 3rd Law
F12 =
–F21.
F13 =
–F31.
F23 =
–F32.
And therefore the sum of the 6 gravitational forces is zero, leaving
(2π)2
[m1r1 + m2r2 + m3r3] = 0
or
[m1r1 + m2r2 + m3r3] = 0
This can be shown to require the point O from which (r1, r2, r3)are measured to be the center of gravity of the three masses. It is no more than an extension of the assertion (section 25) that in a group of objects in which all forces are between one object and another (like the gravity between the masses here), the center of gravity stays fixed. (The same argument is easily extended to 4 or more objects.)
Useful Vector Relations
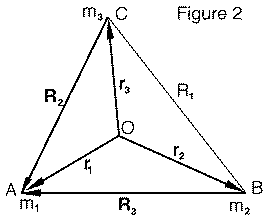
Next, let the sides (R2, R3) of the triangle be regarded as vectors (R2, R3), each directed towards m1 (Figure 2). Then using end-to-end vector addition
r1 = r2 + R3
r1 = r3 + R2
Also, obviously
r1 = r1
Multiply the equations, in their order here, by m2, m3 and m1, and add:
r1 (m1 + m2 + m3) =
[m2r2 + m3r3 + m1r1] +
m3R2 + m2R3
However as shown earlier, the first sum on the right is zero (because O is the center of gravity). If we denoted the total mass by M
(m1 + m2 + m3) = M
then
M r1 = m3R2 + m2R3
We introduce two more vectors
ρ2 = R2 (m3/M)
ρ3 = R3 (m2/M)
with the same directions as (R2, R3). Then this becomes simply
r1=
ρ2 +
ρ3
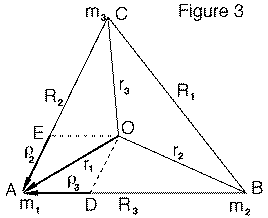 We now interpret the above equation graphically. The vectors (ρ2, ρ3) have the same directions as (R2, R3), and can be represented by segments AE and AD in Figure 3. However, the equation
We now interpret the above equation graphically. The vectors (ρ2, ρ3) have the same directions as (R2, R3), and can be represented by segments AE and AD in Figure 3. However, the equation
r1 =
ρ2 +
ρ3
and the properties of vector addition suggests that suggests that if AE represents ρ2, and we add to it a segment representing ρ3--parallel to AD and of the same length--then the end point will be the point O. (Or in other words, if a 4th point is added to (A,D,E) to form a parallelogram, that point will land on top of O.)
Now comes the trick!
The three forces on the mass m1--namely, F12, F13 and m1(2πT)2r1 --are all in equilibrium. Their vector sum must be zero, and therefore if we line them up end-to-end, they form a closed triangle.
The vectors are parallel to (R2, R3, r1), and therefore to (ρ3, ρ2, r1), so the triangle must be of the same shape as AEO and the lengths of its sides have the same proportions.
The length of a side of a triangle is the magnitude of the vector it represents. So
F12/F13 = ρ3/ρ2
Eliminating fractions by multiplying both sides by (F13ρ2) gives
F12 ρ2= F13 ρ3
Earlier it was shown that
ρ 2 = R2 (m3/M)
ρ3 = R3 (m2/M)
Also, by Newton's Law of gravitation, , if G is the "constant of gravitation"
F12 =
G m1m2/R32
F13 =
G m1m3/R22
Insert all these into the equation F12 ρ2 = F13ρ3 :
[G m1m2m3/M]
R2/R32 =
[G m1m2m3/M]
R3/R22
Dividing both sides by the square brackets
R2/R32 =
R3/R22
and eliminating fractions by multiplying both sides by
R22R32 finally gives
R33 = R23
which implies
R3 = R2
However, we might have gone through the same calculation with mass m2, involving sides R1 and R3 , which would have given R1 = R3. It follows that all three sides of the triangle
ABC must be equal:
R1 = R2 = R3
If this holds, it is relatively easy to show that the 3 equations of equilibrium are satisfied, and given G, even to calculate T. The equilateral triangle ABC thus provides a true equilibrium.
|

 We now interpret the above equation graphically. The vectors (ρ2, ρ3) have the same directions as (R2, R3), and can be represented by segments AE and AD in Figure 3. However, the equation
We now interpret the above equation graphically. The vectors (ρ2, ρ3) have the same directions as (R2, R3), and can be represented by segments AE and AD in Figure 3. However, the equation