Le Noyau AtomiqueLa loi de Planck portait sur l'émission de l'énergie en vrac par la matière chaude . Pour obtenir des informations sur les atomes eux-mêmes il faut cependant comprendre la structure complexe des niveaux d'énergie, en les déduisant des spectres des atomes. Comment se présentent les atomes, et qu'est-ce qui détermine leurs niveaux ?
J.J. Thomson, à l'origine de la découverte de l'électron, pensait que l'atome ressemblait à une masse positivement chargée contenant des électrons négatifs en son sein ("comme les raisins secs dans un plum-pudding"), et d'autres chercheurs réfléchissaient sur les détails de ce modèle. Observé de l'extérieur, les forces électriques en opposition, positives et négatives, s'équilibraient et à une certaine distance tous les atomes apparaissaient comme électriquement neutre. Cependant, on s'attendait à une oscillation des électrons autour de leurs positions d'équilibre, et donc à des rayonnements aux fréquences caractéristiques de leurs oscillations, selon la théorie de Hertz. La formule d'Einstein
suggérait alors un lien entre les fréquences de ces oscillations et celles des rayonnements énergétiques. Cette belle image fut contre-dite par la célèbre expérience d'Ernest Rutherford, originaire de Nouvelle Zélande et pratiquée à Manchester en 1909. On savait que les éléments radioactifs lourds émettent des "particules alpha" ( particules α) , ions rapides d'hélium privés de deux de leurs électrons. Ils présentent donc une charge positive de +2e, deux fois la charge d'un électron –e. Rutherford réussit à détecter individuellement ces ions. Dans l'obscurité totale, si on les dirige sur un écran fluorescent spécial, le point lumineux qu'ils produisent est juste assez suffisant pour être perceptible à l'Ļil adapté à la pénombre, en observant au microscope une petite partie de l'écran. Les particules α possèdent une énergie suffisante pour traverser une fine feuille d'or. Rutherford avait confié à son assistant Hans Geiger (plus tard aidé par Ernest Marsden) le soin d'examiner les perturbations de leur trajectoire au cours du passage à travers ces feuilles. Avec des ions du type de ceux proposés par J.J. Thomson, seules ne peuvent intervenir que les forces électriques des atomes de la feuille d'or, dans l'équilibre des effets des charges positives et négatives. Si les particules coupaient le bord d' un l'atome par sa tranche, les calculs suggéraient une simple inflexion, due à la charge électrique positive.
Geiger et Marsden ont mis en évidence quelque chose de très différent. La plupart des particules α traversent effectivement la feuille avec de très petites inflexions. Mais quelques unes sont largement déviées selon de grands angles , ce qui ne peut s'expliquer que si dans l'atome d'or la charge positive et la majeure partie de sa masse sont situées en un minuscule point très concentré. Ce n'est que lorsque la particule " bombardante " s'approche très fort de ce centre que la répulsion électrique la dévie d'un grand angle ou même la réfléchit. Rutherford a dénommé cette concentration le noyau atomique. Les électrons en restent éloignés, comme les planètes tournant au loin autour du soleil, une comparaison en fait suggérée par Hantaro Nagaoka, au Japon.
En fait les atomes sont (heureusement !) stables. Et pourquoi ?
Le modèle de Bohr de l'atomeLes résultats de Balmer et de Ritz semblaient indiquer que les atomes présentent divers niveaux d'énergie stables, et la formule d'Einstein que l'énergie des niveaux atomiques semble liée à la constante de Planck h, mesurée en Joule-secondes.Une quantité mesurée en Joule-secondes correspond à un moment angulaire. C'est une propriété mécanique (disons comme l'énergie ) de tout objet ou ensemble d'objets en rotation -- même pour la terre, le soleil ou le système solaire. Elle mesure la "quantité de rotation" - prenant en compte la masse impliquée, la distance moyenne et bien sur la vitesse de rotation. C'est une quantité vectorielle, sa direction suivant l'axe de rotation. Les rotations de la terre et du soleil, les mouvements orbitaux des planètes et des lunes, impliquent un moment angulaire. Niels Bohr, jeune physicien danois depuis 1912en Angleterre et finalement collaborateur de Rutherford à l'université de Cambridge, étudia le moment angulaire d'un électron satellisé autour d'un noyau. Il ne pu qu'être supposé, puisque à cause des modifications graduelles des lois de Newton à l'échelle atomique les dimensions du mouvement diminuent en laissant aux électrons la possibilité de conserver des orbites où (pour une raison alors inconnue) aucune énergie ne se perd par émission d'ondes électromagnétiques. Bohr franchit une étape :Ces orbites ne restent sans doute stables que si le moment angulaire du mouvement vaut h fois une certaine valeur, entière. Pour un vaste système, elle peut être des millions de fois plus grande que h, et donc la variation graduelle du moment angulaire (et de l'énergie) est possible. Mais à l'échelle de l'atome d'hydrogène, les possibilités sont rares, et les orbites stables sont tout à fait distinctes, donc également leurs niveaux d'énergie. Pour les orbites circulaires d'un atome d'hydrogène cela colle admirablement, et donne également une valeur cohérente de la constante de Rydberg. En donnant au moment angulaire des valeurs de nh/2π avec n=1,2,3... on obtient des orbites aux énergies exactement concordantes au spectre de l'hydrogène de Balmer (le facteur 2π peut être justifié). Une première étape prometteuse-- mais comment continuer plus loin ? La section ci-dessous est facultative. Elle présente une autre idée à propos de la corrélation des niveaux de quantum par rapport aux valeurs des invariants adiabatiques du mouvement, également mesurés enJoules-sec. Ils ont aussi permis d'arriver correctement aux niveaux de l'hydrogène mais se sont finalement avérés être sans avenir. Les invariants adiabatiques ont été utilisés beaucoup plus tard dans la physique newtonienne des plasmas et des particules chargées piégées dans un champ magnétique, c'est la raison essentielle de les présenter maintenant.(voir liens Web au dernier paragraphe ). Invariants Adiabatiques
Les lois de la physique -- de base et leurs dérivées -- font habituellement appel à des formules précises et quantitatives comme F=ma, E=mc2, E= hν. On rencontre très rarement une loi pas exactement mais approximativement vraie (bien que l'approximation puisse être très bonne), par exemple longtemps valable mais pas pour toute l'éternité. L'invariance adiabatique est de celles là.
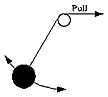
Imaginez un pendule constitué d'un poids attaché à une corde, oscillant dans les deux sens sous l'influence de la pesanteur. A chaque oscillation, pendant la descente, le poids gagne en énergie cinétique, puis après avoir dépassé son niveau le plus bas se met à ralentir et s'arrête brièvement à la fin de l'oscillation. En l'absence de frottement et de résistance de l'air, on s'attend à ce que son énergie totale E (cinétique + potentielle) ne change pas, et que la fréquence μ et période T=1/μ reste également constante. Si la corde passe par une poulie (voyez le dessin) et est lentement remontée, la longueur du pendule diminue graduellement, et comme un pendule plus court présente une fréquence plus élevée μ et une période plus courte T, on s'attend à ce dans ce cas ces quantités varient. Mais l'énergie E augmente également , puisque qu'en tirant la corde un travail est effectué en plus et que donc l'oscillation acquiert de l'énergie. Supposons que la corde soit raccourcie dans une certaine proportion --disons la moitié. On peut démontrer que le changement du rapport E/ν peut être rendu aussi petit qu'on le désire en ralentissant suffisamment le processus. Ce rapport n'est donc pas une vraie constante du mouvement, "invariable", (comme l'énergie dans un pendule non perturbé), mais approximative, un "invariant adiabatique". Cette absence de constante peut être attribuée au fait que la tension sur la corde ne change pas symétriquement à chacune des oscillations -- une petite asymétrie étant à chaque fois ajoutée puisque la corde se raccourcit en continu. Si la traction se ralentit très progressivement, cela réduit considérablement l'asymétrie et ses effets accumulés. Remarquons qu'ici l'invariable adiabatique E/ν s'exprime avec les mêmes valeurs en Joule-sec (c.-à-d. la même combinaison de quantités mesurables ) queh,l'impalpable constante de Planck. Il y a des invariants adiabatiques pour toutes sortes de mouvements périodiques, y compris le mouvement kepleriens, pris comme modèle du mouvement de l'électron autour du noyau. Quelques physiciens, notamment Paul Ehrenfest, ont émis l'hypothèse que les orbites des électrons restaient stables si I, invariable adiabatique de leurs mouvements, correspondait à h fois un certain nombre entier. Pour les orbites circulaires d'un atome, il n'y a qu'un seul invariable adiabatique I, ce qui ne l'autorise à ne prendre que les valeurs I=nh avec n=1,2,3... donnant des orbites dont les énergies sont exactement assorties au spectre de l'hydrogène de Balmer. Il s'est finalement avéré que plutôt que I la quantification du moment angulaire donnait un meilleur arrangement qualitatif pour les atomes de plus d'un électron. Cela est présenté dans la section suivante. Les invariants adiabatiques ont encore étés en vedette dans les années 50, à propos de l'étude du mouvement des ions et des électrons dans les plasmas raréfiés. Un plasma est un gaz suffisamment chaud pour contenir une quantité appréciable d'ions isolés et d'électrons, et s'il est assez raréfié -- par exemple, le plasma de la "magnétosphère" entourant la terre -- ces particules peuvent se déplacer individuellement pendant longtemps avant de se recombiner. En présence d'un champ magnétique suffisamment fort, elles tendent à se développer en spirales autour des lignes du champ magnétique, (qui est un mouvement périodique ) avec ses invariants adiabatiques spécifiques (en fait, plusieurs périodicités et invariants existent). La conservation de ces invariants s'est avérée essentielle au piégeage des particules dans les champs magnétiques de la terre et des autres planètes, et aussi pour beaucoup d'autres phénomènes des plasmas dans l'espace et au laboratoire. Mais cette application des invariants est du ressort "classique" de la mécanique newtonienne, n'impliquant pas la constante de Planck h et porte sur des phénomènes aux dimensions beaucoup plus grandes que l'échelle atomique. Au sujet de cette direction de recherche, voyez "exploration de la magnétosphère terrestre", dont sont tirés ces dossiers. |
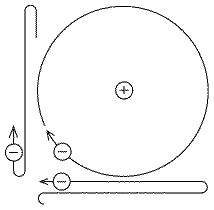Cela ressemble à un système planétaire miniature, avec attraction réciproque du noyau positif et des électrons négatifs jouant le rôle de la pesanteur -- Cette attraction diminue, comme la pesanteur, en raison de l'inverse carré de la distance R, soit 1/R2. Un électron ainsi maintenu devrait obéir aux lois de Kepler, comme une planète attirée par gravitation, et se déplacer sur un cercle ou une ellipse. Mais on peut considérer que son mouvement résulte de la somme de deux oscillations perpendiculaires, chacune atteignant sa plus grande amplitude lorsque l'autre passe au point médian (dans le schéma, ne considérez que la projection du mouvement sur les axes x et y!). Chacun de ces deux mouvements ( indépendants) équivaut à une charge électrique oscillant en va et vient autour d'un point d'équilibre. En raison des lois de Maxwell et de Hertz, ces types d'électrons devraient émettre un rayonnement électromagnétique, atténuant leur énergie qu'ils perdraient rapidement, contrairement aux planètes du système solaire. Leur trajectoire serait spiralée vers l'intérieur, jusqu'à atteindre le noyau.
