Mappa del sito                                                                                                     Programma della lezione


(11)  Grafici ed Ellissi

Le leggi del moto orbitale sono leggi matematiche e non si possono analizzare senza una qualche nozione di matematica. La matematica che verrà usata qui è piuttosto elementare; se avete bisogno di rinfrescarla un po', potete fare clic qui. Altrimenti, potete anche saltare le equazioni e limitarvi a leggere il testo.

La descrizione matematica di una curva

Come si è visto, con il metodo cartesiano viene individuato ogni punto su un piano (come, per esempio, su un foglio di carta) mediante una coppia di numeri, corrispondenti alle sue distanze da due assi perpendicolari. Questi numeri si chiamano le "coordinate" del punto.


Una linea nel piano -- dritta o curva -- contiene molti punti, ciascuno con le sue proprie coordinate (x,y). Spesso esiste una formula ("equazione") che correla x con y: per esempio, le linee rette hanno come equazione

y = ax + b

dove, con ogni coppia di numeri (a,b), positivi, negativi o nulli, si ottiene una certa linea retta. Il disegno dei punti di una linea ottenuta con tale equazione (o con ogni altra relazione, anche ottenuta da valori frutto di osservazioni sperimentali, come, per esempio, i valori della temperatura misurata a vari istanti di tempo), si chiama grafico. Con relazioni più complicate si ottengono i grafici di altre curve: per esempio

y = ax2

dà luogo a una parabola, dove a può essere qualsiasi numero. In genere (anche se non sempre) y si trova separato a primo membro, così che l'equazione ha la forma

y = f(x)

dove f(x) indica "ogni espressione contenente x", o, in termini matematici, è una "funzione di x". Le curve delle figure sono: la retta y = -(2/3)x + 2 e la parabola y = x2. Segue una tabella di alcuni punti delle curve.

 
  Retta:

  x   -1   0   1   2   3   4
  y   8/3   2   4/3   2/3   0   -2/3

Parabola:

  x   -2   -1,5   -1   -0,5   0   0,5   1   1,5   2
  y   4   2,25   1   0,25   0   0,25   1   2,25   4

L'equazione della circonferenza

Nella grande maggioranza dei grafici generati da una formula, l'equazione è data nella forma

y = f(x)

Una tale forma rende molto facile trovare i punti di un grafico. Tutto quello che occorre fare è scegliere un valore di x, calcolare f(x) (= una qualunque espressione contenente x) e si ottiene il corrispondente valore di y.

Tuttavia, ogni equazione contenente x e y può essere considerata come una proprietà valida per tutti i punti del grafico. La differenza sta nel fatto che, con equazioni molto più complicate, dopo aver scelto x, trovare il corrispondente valore di y può essere molto laborioso (e talvolta è più semplice scegliere y e poi calcolare x).

Forse il grafico di questo genere che è più noto è quello di una circonferenza di raggio R, la cui equazione è

x2  +  y2  =   R2

Disegnamo una circonferenza di raggio R centrata nell'origine O di un sistema di assi (x,y). Dato un punto P della circonferenza, specificato dai valori (x,y), tracciamo la perpendicolare da P al punto A sull'asse x. Si avrà

x = OA        y = AP       R = OP

In questo caso x e/o y possono essere negativi, se si trovano alla sinistra dell'asse y o al di sotto dell'asse x, ma, qualunque sia il segno, x2 e y2 saranno sempre entrambi positivi. Poiché il triangolo OAP ha un angolo di 90°, dal teorema di Pitagora, qualunque sia la scelta di P, vale sempre la seguente relazione:

OA2  +  AP2  =   OP2

Poiché questa può anche essere scritta come

x2  +  y2  =   R2

l'equazione della circonferenza è soddisfatta da ogni punto che ne faccia parte. Per esempio, se il grafico è definito dall'equazione:

x2  +  y2  =   25

questa equazione è soddisfatta da tutti i punti della seguente tabella:

  x   5   4   3   0   -3   -4   -5   -4   -3   0   3   4 ( 5 )
  y   0   3   4   5   4   3   0   -3   -4   -5   -4   -3 ( 0 )

L'equazione dell'ellisse

L'equazione della circonferenza esprime ancora la stessa relazione se si dividono entrambi i membri per R2:

(x2/R2)  +  (y2/R2)  =   1

L'equazione di un'ellisse si ottiene con una piccola variante:

(x2/a2)  +  (y2/b2)  =   1

dove (a,b) sono due numeri dati, per esempio (8,4). Che aspetto avrà il grafico? Vicino all'asse x, y ha un valore molto piccolo e l'equazione diventa molto simile a

(x2/a2)  =   1

Da cui

x2 = a2 e quindi x = a  oppure x = –a   (talvolta combinato nell'espressione x = ±a)

Nell'intorno dell'asse x, il grafico quindi rassomiglia a un tratto di circonferenza di raggio a, la cui equazione

(x2/a2)  +  (y2/a2)  =   1

diventa molto simile a x2 = a2 in questa regione. Esattamente nello stesso modo si può vedere che, nelle vicinanze dell'asse y, dove x è piccolo, il grafico taglia l'asse nei punti y = ±b e la sua forma in quell'intorno rassomiglia a quella di una circonferenza di raggio b.

Un esempio

Disegnamo l'ellisse

(x2/64)  +  (y2/16)  =   1

Sappiamo già che essa taglia gli assi nei punti x = ±8 e y = ±4. Aggiungiamo ora qualche altro punto:

(1)   Scegliamo y = 2 . Per cui, dall'equazione

(x2/64)  +  (4/16)  =   1

Sottraiamo 1/4 da entrambi i membri

(x2/64)  =3/4

Estraendo la radice quadrata, e usando solo 3-4 cifre decimali:

x/8 = √(3)/√(4) = 1,732/2 = 0,866

da cui, con ragionevole accuratezza  x = 6,93.

(2)   Scegliamo y = 3 .
(x2/64)  +  (9/16)  =   1

Sottraiamo 9/16 da entrambi i membri

(x2/64)  =7/16

Estraendo la radice quadrata (con un'accuratezza di 3-4 cifre decimali):

x/8 = √(7)/√(16) = 2,6457/4 = 0,6674

Da cui, approssimativamente  x = 5,29.

Anche qui, x e y hanno entrambi i segni. Otteniamo così 12 punti, sufficienti per un grafico grossolano:

  x   8   6,93   5,29   0   -5,29   -6,93   -8   -6,93   -5,29   0   5,29   6,93 ( 8 )
  y   0   2   3   4   3   3   0   -2   -3   -4   -3   -2 ( 0 )

Un modo diverso di vedere un'ellisse

  Un'ellisse è il luogo dei punti
  per i quali  R1 + R2   ha lo
  stesso valore.
L'ellisse era già familiare agli antichi scienziati greci (che si chiamavano "filosofi", amanti del sapere), ma la definivano in modo diverso. Per loro l'ellisse era l'insieme di tutti i punti (su un piano) per i quali la somma delle distanze R1 + R2 da due dati punti era la stessa (ved. disegno).

Era la naturale estensione della definizione di circonferenza, che è l'insieme dei punti (in termini matematici "il luogo dei punti") che sono alla stessa distanza (il raggio R) da un dato punto (il centro). Un punto e la distanza R definiscono la circonferenza, due punti e la distanza R1 + R2 definiscono un'ellisse.

I due punti sono detti i fuochi dell'ellisse, ed essi sono importanti poiché Keplero trovò che il Sole occupa sempre un fuoco dell'ellisse orbitale, e non (come si potrebbe pensare) il centro -- cioè l'origine, nel caso in cui l'ellisse sia espressa dalla sua equazione in un sistema di assi perpendicolari (x,y).

(x2/a2)  +  (y2/b2)  =   1

I fuochi sono sempre situati sul più lungo dei due assi di simmetria dell'ellisse -- gli assi (x,y) nel caso che si sia usata l'equazione qui sopra -- cioè l'asse maggiore dell'ellisse. Se a è più grande di b, l'asse maggiore è situato lungo l'asse x, e lasciamo al lettore il compito di dimostrare che in tal caso

R1 + R2 = 2a

[Suggerimento: Fate uno schizzo dell'ellisse e degli assi che lo definiscono, segnate uno dei punti dove l'ellisse taglia l'asse x, ed esaminate i valori R1 e R2 relativi a quel punto].
Il valore di a in un'orbita ellittica è chiamato in astronomia il semiasse maggiore ed è uno dei sei elementi orbitali che definiscono il moto secondo le leggi di Keplero.

Bisbigli nel Campidoglio di Washington

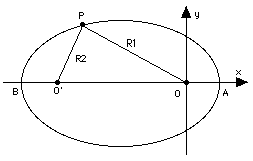
I fuochi di un'ellisse hanno una interessante proprietà. Un ellissoide di rivoluzione è la figura tridimensionale ottenuta facendo ruotare un'ellisse attorno a uno dei suoi assi. Se si costruisce un ellissoide cavo di tale forma e si argenta la sua superficie interna perché diventi riflettente come uno specchio, allora, se una sorgente di luce viene posta in uno dei fuochi, tutti suoi raggi andranno a convergere nell'altro fuoco. Anche se viene argentata soltanto una parte dell'ellissoide, tutta la luce che colpisce quella parte verrà ancora concentrata nell'altro fuoco.

Anche le onde sonore si comportano come quelle luminose. La sala del Campidoglio a Washington, dove una volta si riuniva la Camera dei Rappresentanti, ha il soffitto a forma di quadrante di ellissoide (cioè la metà di una metà di un ellissoide), con i suoi fuochi vicino al pavimento. Fu costruto così per ragioni architettoniche, circa 200 anni fa, ma il risultato è che una persona che si trovi in uno dei due fuochi riesce ad ascoltare qualunque parola pronunciata nell'altro fuoco, anche se appena bisbigliata. Possiamo supporre che l'ideatore, Daniel Webster, si sedesse in uno dei quei punti e sfruttasse questa proprietà particolare.

Oggi la Camera dei Rappresentanti ha molti più membri, usa per le sue riunioni una sala molto più grande, e quella antica sala di riunione è ora un museo dove sono esposte le statue di Americani insigni.

Ogni anno molte migliaia di visitatori vengono guidati attraverso quella sala. A un certo momento, durante la visita, un gruppo di visitatori si raccoglie in prossimità di uno dei due fuochi (indicati da una targa di ottone sul pavimento) per ascoltare i bisbigli della loro guida che si è posizionata sull'altro fuoco. Tra l'altro, Samuel Morse, l'inventore del telegrafo elettrico, dipinse un quadro di quella sala, con tutti suoi occupanti ben identificabili. Una copia del quadro e la sua storia sono esposte nella sala, mentre il quadro originale è conservato nella Galleria Corcoran a Washington.

Domande poste dagli utenti:   L'equazione di una parabola  

Il prossimo argomento, per coloro che
hanno familiarità con la trigonometria -- #11a   Le ellissi e la prima legge di Keplero

Altrimenti, il prossimo argomento è: #12  La seconda legge di Keplero

            Cronologia                     Glossario                     Torna alla pagina iniziale

Autore e Curatore:   Dr. David P. Stern
     Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese, per favore!):   stargaze("chiocciola")phy6.org

Traduzione in lingua italiana di Giuliano Pinto

Aggiornato al 21 Marzo 2005