Galileo probabilmente fu il primo ad osservare attentamente in che modo gli oggetti cadono a terra. Secondo la leggenda, egli salì in cima alla torre pendente di Pisa e da lassù fece cadere simultaneamente delle sfere pesanti e leggere, e notò che arrivavano a terra nello stesso istante. Egli così dimostrò, contrariamente a quanto sostenevano gli antichi, che oggetti ("corpi") pesanti e leggeri cadevano con la stessa velocità. Gli studi di Galileo suscitarono grande interesse, poiché si applicavano non soltanto alla semplice caduta dei corpi -- come la caduta di una mela da un albero, che sembra abbia ispirato Newton -- ma riguardavano un argomento molto pratico come la traiettoria delle palle di cannone.
L'accelerazione
Un oggetto lasciato cadere inizia la sua caduta piuttosto lentamente, ma poi acquista via via sempre più velocità (accelera) col passare del tempo. Galileo dimostrò che (trascurando la resistenza dell'aria) oggetti leggeri e pesanti accelerano in modo costante mentre cadono, cioè la loro velocità aumenta a ritmo costante. La velocità di una sfera lasciata cadere da una posizione elevata aumenta ogni secondo di una quantità costante, indicata in genere con la lettera g minuscola (iniziale di "gravità"). Con notazioni moderne (usando le convenzioni dell'algebra, in cui simboli o numeri scritti di seguito si intendono moltiplicati tra loro) la sua velocità è
all'inizio -- 0 (zero)
dopo 1 secondo-- g metri/secondo
dopo 2 secondi-- 2g metri/secondo
dopo 3 secondi-- 3g metri/secondo
e così via. Tutto questo è un po' modificato dalla resistenza dell'aria, che diventa importante a velocità molto elevate e in genere fissa un limite superiore ("velocità terminale") alla velocità di caduta -- un limite che è molto più basso per chi usa un paracadute rispetto a chi non lo usa.
Il numero g è prossimo a 10 -- più precisamente pari a 9,79 all'equatore, 9,83 ai poli, e valori intermedi nelle altre zone -- ed è noto come "accelerazione di gravità". Se la velocità aumenta di 9,81 m/s ogni secondo (un buon valor medio), si dice che g è uguale a "9,81 metri al secondo per secondo" o concisamente 9,81 m/s2.
Aggiungendo una velocità iniziale
Supponiamo ora di dare alla sfera una velocità iniziale u verso l'alto oppure verso il basso. Se scegliamo come positive le distanze verso il basso, la velocità dovuta alla gravità sarà sempre positiva, mentre u sarà positiva se diretta verso il basso, e negativa se diretta vero l'alto.
Con questa convenzione, le osservazioni mostrano che u deve essere sempre aggiunta alla velocità dovuta alla gravità, per cui la velocità nei secondi successivi (come è riportato sopra) sarà
u, u+g, u+2g, u+3g . . .
e in generale, dopo t secondi, con gt che significa "g volte t" u + gt.
La distanza percorsa
Si può dimostrare che la distanza percorsa dalla sfera sarà la stessa di quella di una sfera che si muova con una velocità "media" v(media) uguale alla metà della somma della velocità iniziale e della velocità finale. Per la sfera in caduta libera dell'esempio precedente, dopo t secondi si avrà
v(media) = (1/2)[u + (u+gt)]
per cui la distanza percorsa è
distanza = t v(media) = ut + (1/2) gt2
L'esperimento di Galileo
Il libro "La particella di Dio" scritto dal premio Nobel Leon Lederman insieme a Dick Teresi (un buon libro se riuscite a sopportare il tono irriverente e un umorismo un po' banale) racconta di come Galileo dimostrò che il moto verso il basso di una sfera sotto l'azione della gravità ha una accelerazione costante, e che, partendo dalla quiete (u = 0), la sfera percorre distanze crescenti (come mostrato nella formula precedente) in proporzione al quadrato del tempo trascorso.
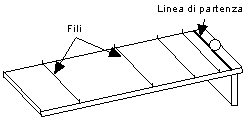
Poiché una caduta verticale sarebbe stata troppo rapida perché Galileo potesse osservarla accuratamente, egli rallentò il moto facendo rotolare la sfera lungo una tavola inclinata. Lungo la tavola, egli dispose trasversalmente un certo numero di fili orizzontali ben tesi, in modo che la sfera facesse risuonare un clic ogni volta che attraversava un filo. Quindi Galileo si mise a spostare i fili su e giù lungo la tavola, finché i suoni dei clic fossero ugualmente spaziati nel tempo.
Se ora l'accelerazione era a (molto minore di g) e il tempo t era misurato in clic, dalla formula precedente, partendo da una sfera in quiete (u= 0) si ottiene per la distanza S percorsa
Dopo un clic S = (a/2) 12 = a/ 2
Dopo due S = (a/2) 22 = 2a
Dopo tre S = (a/2) 32 = 4,5 a
e così via. Il rapporto tra le distanze deve essere quello dei numeri quadrati 1, 4, 9, 16, 25. . . e questo è quanto Galileo confermò. Se si convertono i clic in secondi, tenendo conto dell'angolo di inclinazione della tavola e anche del fatto che la sfera rotolava (una teoria che non era conosciuta ai tempi di Galileo), è possibile in linea di principio calcolare g da a.
Un esperimento simile a quello di Galileo, facile da realizzarsi, è descritto alla fine di questo file.
Le cascate e il gioco del "baseball"
Se inoltre si dà alla sfera anche una velocità iniziale orizzontale w, il suo moto orizzontale continua indisturbato, avanzando di una distanza w ogni secondo, anche mentre la sfera sta cadendo verso il basso (trascurando la resistenza dell'aria). I due moti si svolgono simultaneamente, così che la sfera descrive una curva che diventa sempre più ripida poiché la velocità verso il basso (verticale) aumenta, mentre quella orizzontale rimane costante. E' questo il modo in cui si muovono le gocce d'acqua di una cascata, producendo, vista in sezione, la sua caratteristica forma (ved. figura a sinistra).

La situazione che abbiamo visto tante volte nei cartoni animati di "Road Runner", dove Willy Coyote corre oltre un precipizio, rimane immobile nello spazio (prima di rendersi conto di stare nel vuoto), e poi piomba giù verticalmente, è pura fantasia, completamente contraria alle leggi della fisica. In realtà, anche in quel caso i due moti si svolgono simultaneamente. Allo stesso modo, un proiettile di fucile sparato contro un bersaglio comincia a cadere nell'istante in cui esce dalla canna. Regolando l'alzo del fucile in base alla distanza, si sposta il puntamento al di sopra della direzione del mirino, in modo che, alla distanza opportuna, la caduta del proiettile lo porti correttamente al livello del bersaglio.
Per un sasso lanciato verso l'alto, u è negativa, come lo sono le distanze verticali al di sopra del punto di lancio. In tal caso, sia û = -u un numero positivo. Allora, dopo t secondi
velocità = (-û + gt) m/s
All'inizio t è piccolo e la velocità è negativa, indicando che il sasso sta viaggiando verso l'alto. Nell'istante in cui
gt = û
la somma è zero e per un brevissimo istante il sasso è fermo, al culmine della sua traiettoria. In quel momento
t = û/g
e se si usa questo valore nella formula della distanza, si trova qual'è la massima altezza raggiunta. Infine, se si aggiunge a questo moto una velocità orizzontale costante w, si ottiene il moto di una palla di cannone o di una palla nel gioco del "baseball".
A proposito della resistenza dell'aria
Le formule riportate sopra valgono per una palla di cannone ideale che non incontri la resistenza dell'aria. Nella pratica reale, invece, la resistenza dell'aria modifica il moto e bisogna tenerne conto, specialmente nel caso della caduta di un oggetto leggero, come per esempio una piuma. In una dimostrazione scientifica popolare per secoli, si facevano cadere simultaneamente una piuma e una moneta in un tubo da cui era stata tolta l'aria: si vedevano i due oggetti cadere alla stessa velocità.
Una tale dimostrazione fu anche ripetuta sulla superficie lunare da David Scott, uno degli astronauti della missione Apollo. Non solo sulla Luna non c'è atmosfera, ma la sua gravità è diverse volte minore di quella terrestre, rendendo la caduta più lenta e quindi più facile da osservare. Davanti a una telecamera, l'astronauta lasciò cadere contemporaneamente un martello e una piuma, e tutti gli spettatori sulla Terra, guardando sullo schermo televisivo, videro i due oggetti cadere insieme.
Secondo un aneddoto, Scott tentò prima l'esperimento fuori dal campo visivo della telecamera, per esssere sicuro che funzionasse. Non funzionò! L'elettricità statica aveva fatto aderire la piuma al guanto della tuta spaziale. Mentre stava ancora cercando di risolvere il problema, a Scott venne chiesto di guardare verso la telecamera, e questa volta l'esperimento funzionò perfettamente.
(Forse si tratta solo di una leggenda moderna; ma, in caso contrario, merita di essere ricordata!).