|
Tuttavia, per il terzo principio della dinamica
F12 =
–F21.
F13 =
–F31.
F23 =
–F32.
E quindi la somma delle 6 forze gravitazionali è zero, lasciando perciò
(2π)2
[m1r1 + m2r2 + m3r3] = 0
oppure
[m1r1 + m2r2 + m3r3] = 0
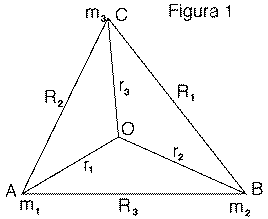
Si può dimostrare che tutto questo richiede che il punto O, da cui vengono misurati (r1, r2, r3), sia il baricentro delle tre masse. Questo non è altro che l'estensione dell'affermazione (ved. la sezione 25) secondo cui, in un gruppo di oggetti in cui tutte le forze sono soltanto quelle che si esercitano tra di essi (come in questo caso l'attrazione gravitazionale tra le masse), il baricentro si mantiene fisso (lo stesso discorso può essere esteso facilmente a 4 o più oggetti).
Utili relazioni tra vettori
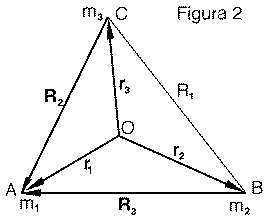
Adesso consideriamo i lati (R2, R3) del triangolo come se fossero tutti e due dei vettori (R2, R3), ciascuno diretto verso m1 (ved. Figura 2). Effettuandone la somma vettoriale, otteniamo
r1 = r2 + R3
r1 = r3 + R2
E, ovviamente
r1 = r1
Moltiplicando le equazioni, nell'ordine qui riportato, per m2, m3 e m1, e poi sommandole:
r1 (m1 + m2 + m3) =
[m2r2 + m3r3 + m1r1] +
m3R2 + m2R3
Tuttavia, come si è visto precedentemente, la prima somma a secondo membro è zero (poiché O è il baricentro). Se indichiamo con M la massa totale:
(m1 + m2 + m3) = M
allora
M r1 = m3R2 + m2R3
Introduciamo ora altri due vettori
ρ2 = R2 (m3/M)
ρ3 = R3 (m2/M)
orientati nella stessa direzione di (R2, R3). Il tutto diventa semplicemente
r1=
ρ2 +
ρ3
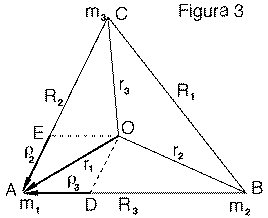Interpretiamo ora graficamente questa equazione. I vettori (ρ2, ρ3) hanno la stessa direzione di (R2, R3), e possono essere rappresentati dai segmenti AE e AD in Figura 3. Tuttavia l'equazione
r1 =
ρ2 +
ρ3
e le proprietà della somma tra vettori suggeriscono che, se AE rappresenta ρ2, e sommiamo ad esso un segmento che rappresenta ρ3 -- parallelo a AD e della stessa lunghezza -- allora la sua estremità coinciderà con il punto O (oppure, in altre parole, se si aggiunge un 4o punto a (A,D,E) per formare un parallelogramma, quel punto andrà a finire in O).
Adesso viene il trucco!
Le tre forze che agiscono sulla massa m1 -- cioè F12, F13 e m1(2πT)2r1 -- sono tutte in equilibrio. La loro somma vettoriale deve essere zero, e quindi, se disponiamo tutti e tre i vettori con l'estremità dell'uno sull'inizio dell'altro, otteniamo un triangolo chiuso.
I vettori sono paralleli a (R2, R3, r1), e perciò anche a (ρ3, ρ2, r1), per cui il triangolo dovrà avere la stessa forma del triangolo AEO, e le lunghezze dei suoi lati saranno nelle stesse proporzioni (cioè i due triangoli sono "simili").
La lunghezza di un lato del triangolo è proporzionale alla grandezza del vettore che rappresenta. Per cui
F12/F13 = ρ3/ρ2
Eliminando le frazioni, moltiplicando ambo i membri per (F13ρ2) si ottiene
F12 ρ2= F13 ρ3
Precedentemente era stato dimostrato che
ρ 2 = R2 (m3/M)
ρ3 = R3 (m2/M)
Inoltre, per la legge della gravitazione di Newton, se G è la "costante di gravità"
F12 =
G m1m2/R32
F13 =
G m1m3/R22
Sostituendo queste espressioni nell'equazione F12 ρ2 = F13ρ3 :
[G m1m2m3/M]
R2/R32 =
[G m1m2m3/M]
R3/R22
Dividendo entrambi i membri per le espressioni tra parentesi quadre
R2/R32 =
R3/R22
ed eliminando le frazioni, moltiplicando entrambi i membri per
R22R32 si ottiene infine
R33 = R23
da cui
R3 = R2
Comunque, avremmo potuto svolgere lo stesso calcolo relativamente alla massa m2, considerando i lati R1 e R3, e avremmo ottenuto R1 = R3. Ne deriva quindi che tutti e tre i lati del triangolo ABC devono essere uguali:
R1 = R2 = R3
Se vale questa relazione, è relativamente facile dimostrare che le 3 equazioni di equilibrio sono soddisfatte, e, conoscendo G, si può calcolare T. Il triangolo equilatero ABC fornisce così il completo equilibrio.
|
