|
Si può dimostrare che l'ellisse di trasferimento di Hohmann è il modo più efficiente di usare la spinta di un razzo per raggiungere Marte. Con altre traiettorie ci si può arrivare più rapidamente, ma occorrerebbe una maggiore spinta iniziale alla partenza e una maggiore spinta di aggiustamento all'arrivo, incluso forse un cambiamento di direzione. C'è qualche controindicazione? Soltanto una: una condizione molto stringente sulle posizioni relative della Terra e di Marte al momento del lancio. Come si vedrà, queste condizioni si verificano soltanto una volta ogni circa 26 mesi. Anche per ritornare indietro da Marte alla Terra si può usare l'ellisse di Hohmann, ma, anche in questo caso, i pianeti devono essere posizionati esattamente al momento del lancio. Se degli astronauti terrestri dovessero atterrare su Marte, si dovrebbe scegliere tra aspettare oltre un anno perché si verifichino le condizioni necessarie, oppure seguire una via più diretta, ma meno economica, per il ritorno a casa.
Nei paragrafi seguenti viene calcolato questo tempo di attesa. Verrà utilizzato il concetto di periodo sinodico di Marte, cioè il suo periodo orbitale come viene visto dalla Terra in orbita.
Le orbite di Hohmann verso Marte e al ritorno
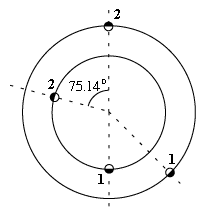
Nel disegno a sinistra, i cerchi indicano il moto della Terra (ellisse più interna) e di Marte (ellisse più esterna) lungo le loro orbite. Come è stato mostrato nella sezione (21b), quando un'astronave viene lanciata dalla Terra verso Marte, i due pianeti devono trovarsi nei punti indicati con "1". Dopo 0,70873 anni, l'astronave arriva nelle vicinanze di Marte, il quale nel frattempo si è spostato nel punto indicato con "2". Dove si trova la Terra in quel momento? In un anno la Terra percorre 360 gradi, per cui in 0,70873 anni avrà percorso
Avrà quindi raggiunto la posizione "2" sul cerchio più interno, 75,14° oltre la posizione di Marte. Va notato che la Terra ha sorpassato Marte -- al lancio (posizione "1") stava indietro rispetto a Marte, ma ora sta avanti. Come è mostrato dalla 3ª legge di Keplero, più un pianeta è vicino al Sole, e più rapidamente percorre la sua orbita, e nel nostro caso la Terra è più vicina al Sole di quanto non lo sia Marte. Supponiamo che l'astronave che è arrivata su Marte sia una sonda automatica, che raccolga dei campioni e riparta immediatamente per il suo viaggio di ritorno. Lanciata dal punto (2), dopo essere sfuggita alla gravità del pianeta, l'astronave seguirà ancora una ellisse di trasferimento di Hohmann, che è l'immagine speculare di quella percorsa nel viaggio di andata verso Marte (ved. disegno qui sotto).
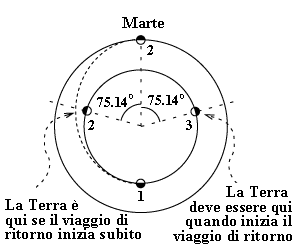
Il viaggio di ritorno inizia con una spinta all'indietro di 2,545 km/s, per ridurre la velocità orbitale dell'astronave da V3 a V2. Pertanto, dopo 0,70873 anni, essa arriverà nel punto indicato con (1) con una velocità V1, che deve essere ridotta al valore della velocità orbitale della Terra V0 mediante una spinta all'indietro di 2,966 km/s. Purtroppo... la Terra non starà lì ad aspettare!
Vediamo dove dovrebbe stare la Terra al momento del lancio da Marte, perché alla fine del viaggio di ritorno venga incontrata al momento giusto. Il viaggio di ritorno, essendo costituito dalla metà dell'ellisse di Hohmann, durerà 0,70873 anni, e durante questo tempo (come è stato calcolato precedentemente) la Terra avrà percorso un arco di orbita di 255,14°. Per incontrare il razzo al suo ritorno, quando raggiungerà l'orbita terrestre nel punto (1), la Terra deve trovarsi -- al momento dell'inizio del viaggio di ritorno da Marte -- 255,14° indietro rispetto al punto "1" della sua orbita. Questo la posiziona nel punto (3), 75,14° indietro rispetto alla posizione di Marte, non nella posizione (2) dove la Terra è 75,14° in avanti rispetto a Marte. Poiché la Terra e Marte cambiano continuamente la loro posizione relativa, è logico che, se ritardiamo sufficientemente il viaggio di ritorno, la Terra si sposterà dalla posizione (2) rispetto a Marte alla posizione (3), e in quel momento può iniziare il viaggio di ritorno. Calcoliamo ora quel tempo di attesa. Per semplificare il calcolo dell'attesa, calcoliamo la velocità relativa di rivoluzione tra la Terra e Marte intorno al Sole.
Ogni anno, la Terra aumenta il suo vantaggio su Marte di
Se Marte e la Terra iniziano un'orbita fianco a fianco, dopo 2,13353 anni essi si troveranno di nuovo fianco a fianco. Dal punto di vista di un osservatore sulla Terra, questo è il tempo necessario a Marte per compiere un giro completo nel cielo. Tale tempo è chiamato periodo sinodico di Marte e dura circa 25,6 mesi. Il resto è facile. Perché la Terra cambi la sua posizione rispetto a Marte da (2) a (3), occorre che la Terra avanzi (rispetto a Marte) di Per avanzare di 360° occorrono 2,13353 anni, e quindi per avanzare di quell'angolo occorrono
Un calcolo più accurato dà 459 giorni (il nostro calcolo conteneva delle approssimazioni). Quando il razzo nel suo viaggio di ritorno arriverà nelle vicinanze della Terra la sorpasserà, poiché la sua velocità V1 supera quella della Terra di circa 3 km/s. Prima di scendere in tutta sicurezza al suolo, l'astronave dovrà smaltire la velocità v0 dovuta all'attrazione terrestre, pari a circa 11,3 km/s. Tuttavia, se il rientro a volo radente nell'atmosfera ha un "corretto angolo", l'energia cinetica in eccesso sarà dissipata tranquillamente in calore, senza la necessità di usare razzi frenanti.
Riflessioni finaliLe nostre considerazioni riguardavano soltanto orbite circolari attorno al Sole, a velocità pressoché costante. Il moto relativo della Terra e di Marte in cielo è molto più variabile, poiché la distanza Terra-Marte varia continuamente. In effetti, quando la Terra è nel punto più vicino a Marte e lo sorpassa, Marte sembrerà (per un breve periodo) muoversi all'indietro rispetto alle stelle. Il periodo totale resta comunque di 25,6 mesi, piuttosto diverso dall'effettivo periodo orbitale di Marte attorno al Sole che è di 1,8822 anni = 22,6 mesi. Considerando tutte queste complicazioni, non possiamo fare a meno di apprezzare la sottigliezza del lavoro di Copernico e di Keplero, che sono riusciti ad estrarre modelli chiari e regolari del moto, partendo da quelli molto meno regolari dei pianeti attraverso il cielo. Domande poste dagli utenti: Pianeti che si sorpassano |