(Q-5) Il nucleo atomico e

il primo modello dell'atomo di Bohr

suggerisce allora un collegamento tra la frequenza di oscillazione e l'energia irradiata.

    Questo bel modello fu contraddetto da un notevole esperimento effettuato a Manchester nel 1909 da Ernest Rutherford, originario della Nuova Zelanda. Era noto a quei tempi che gli elementi radioattivi pesanti emettevano le "particelle alfa" (particelle α), ioni veloci di elio privati dei loro elettroni. Questo li rendeva dotati di una carica positiva di +2e, cioè due volte la carica dell'elettrone –e.

    Rutherford sapeva come rivelare singolarmente questi ioni. Nell'oscurità completa, quando essi colpivano uno schermo fluorescente preparato appositamente, si produceva un lampo abbastanza intenso da essere visto da un occhio adattato all'oscurità, osservando una piccola parte dello schermo con un microscopio. Si trovò che le particelle α avevano abbastanza energia da penetrare in un sottile foglio di oro, e Rutherford quindi incaricò il suo assistente Hans Geiger (in seguito aiutato da Ernest Marsden) di esaminare in che modo il passaggio attraverso il foglio d'oro influenzasse il loro moto.

    Con un atomo del tipo di quello proposto da J.J. Thomson, gli ioni non avrebbero risentito di nessuna forza elettrica all'esterno dell'atomo di oro, dove gli effetti delle cariche positive e negative si sarebbero cancellati tra loro. Se gli ioni passavano vicini al bordo dell'atomo, i calcoli suggerivano che la carica positiva distribuita avrebbe potuto deviare leggermente il loro percorso.

    Quello che Geiger e Marsden osservarono, tuttavia, fu molto differente. La maggior parte delle particelle α in realtà passavano attraverso il foglio soltanto con una piccolissima deflessione. Però alcune venivano sparpagliate su grandi angoli, in un modo che poteva essere spiegato soltanto supponendo che la carica positiva degli atomi di oro e la maggior parte della loro massa formasse una minuscola concentrazione quasi puntiforme. In tal caso, soltanto quando la particella, usata per bombardare l'atomo, era in grado di avvicinarsi talmente a tale punto, le forze elettriche repulsive potevano defletterla di un grande angolo o addirittura respingerla all'indietro. Rutherford chiamò questa concentrazione il nucleo dell'atomo. Gli elettroni si trovavano molto più lontani, come i pianeti orbitanti lontano dal Sole, un paragone in realtà suggerito da Hantaro Nagaoka in Giappone.

    Sembrava come un sistema planetario in miniatura, in cui l'attrazione tra il nucleo positivo e gli elettroni negativi prendeva il posto della gravità -- un'attrazione che, come la gravità, diminuiva con l'inverso del quadrato della distanza R, cioè come 1/R². Un elettrone in questa situazione doveva obbedire alle leggi di Keplero, come un pianeta attratto dalla gravità, e doveva muoversi lungo una circonferenza o lungo un'ellisse. Il suo moto può essere considerato come la somma di due oscillazioni perpendicolari, dove ciascuna raggiunge la sua massima ampiezza nel momento in cui l'altra si trova nel suo punto mediano (nella figura, si considerino soltanto le proiezioni del moto sugli assi x e y!).

    Ciascuno di questi due (indipendenti) movimenti è equivalente all'oscillazione avanti e indietro di una carica elettrica attorno al suo punto di equilibrio. Tuttavia, per le leggi di Maxwell e di Hertz, un tale elettrone dovrebbe emettere una radiazione elettromagnetica, e quindi ridurre la sua energia. Per questo motivo, a differenza dei pianeti del Sistema Solare, gli elettroni perderebbero rapidamente la loro energia irradiandola e quindi cadrebbero a spirale verso il nucleo.

Invece gli atomi sono (per fortuna!) stabili. Come mai?

    Una quantità misurata in joule-secondo era il momento angolare. È questa una proprietà meccanica (come lo è, per esempio, l'energia) di ogni oggetto o sistema di oggetti in rotazione -- anche un sistema come quello della Terra, del Sole o dell'intero Sistema Solare. Questa proprietà misura la "quantità di rotazione" totale -- che tiene conto della massa, della sua distanza media dall'asse di rotazione, e naturalmente della velocità di rotazione. Si tratta di una quantità vettoriale, e la sua direzione è quella dell'asse di rotazione.

    La rotazione della Terra e del Sole e i moti orbitali dei pianeti e dei loro satelliti comportano un momento angolare. Un giovane fisico danese, Niels Bohr, che arrivò in Inghilterra nel 1912 e andò a lavorare con Rutherford all'Università di Cambridge, studiò il momento angolare di un elettrone in orbita attorno a un nucleo. Si supponeva a quei tempi che, quando le dimensioni si riducevano alla scala atomica, le leggi di Newton si modificassero gradualmente, consentendo orbite in cui (per qualche ragione ancora ignota) non venisse perduta energia con l'emissione di onde elettromagnetiche. Bohr andò oltre: forse le orbite erano stabili quando il momento angolare era uguale ad h volte un certo numero intero. In un sistema di grandi dimensioni, questo numero poteva essere milioni di volte più grande di h, per cui la legge consentiva al momento angolare (e all'energia) di variare in modo quasi continuo. Invece, alla scala dell'atomo di idrogeno, le possibilità erano poche, e le orbite stabili ben distinte, e così pure i loro livelli energetici.

    Per le orbite circolari in un atomo di idrogeno questo modello funzionava egregiamente, e dava anche un valore coerente per la costante di Rydberg. Assegnando al momento angolare i valori nh/2π, con n=1,2,3..., si ottengono orbite con energie che si accordano perfettamente con lo spettro dell'idrogeno di Balmer (il fattore 2π può essere spiegato). Un inizio molto promettente, ma come proseguire?

    Le leggi della fisica -- quelle fondamentali e quelle da esse derivate -- normalmente offrono degli enunciati precisi e quantitativi, come per esempio F=ma, E=mc², E= hν. Molto raramente si incontra una legge secondo cui qualcosa è vero approssimativamente, ma non del tutto (anche se l'approssimazione può essere molto buona), per esempio, che sia valida per un tempo lungo ma non per tutta l'eternità. L'invarianza adiabatica è qualcosa di questo genere.

    Immaginiamo un pendolo formato da un peso legato a una cordicella, che oscilla avanti e indietro sotto l'influenza della gravità. In ogni oscillazione, quando il peso scende nel punto più basso del suo percorso, esso guadagna energia cinetica, poi, quando ha superato quel punto, rallenta di nuovo, fino a fermarsi brevemente nel punto più alto dell'oscillazione. In assenza di attrito dell'aria, ci si aspetta che l'energia totale E (cinetica + potenziale) rimanga invariata, e che la frequenza ν e il periodo T=1/ν rimangano anch'essi costanti.

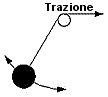
    Se la cordicella passa per una puleggia (ved. figura) e si comincia a tirarla lentamente, la lunghezza del pendolo gradualmente diminuirà e, poiché un pendolo più corto ha una frequenza ν più alta e un periodo T più corto, ci si aspetta che anche queste quantità cambino. Però anche l'energia E aumenta, poiché si è compiuto un ulteriore lavoro contro la forza che tira la cordicella, per cui l'oscillazione acquista energia. Supponiamo che la corda sia tirata fino a che la sua lunghezza sia ridotta di una certa frazione -- diciamo della metà. Si può dimostrare che la variazione del rapporto E/ν può essere fatta piccola a piacere rendendo il processo di trazione abbastanza lento.

    Questo rapporto non è una vera costante del moto o "invariante" (come l'energia di un pendolo imperturbato), ma di tipo approssimativo -- un "invariante adiabatico". La poca costanza può essere attribuita al fatto che la tensione della cordicella ad ogni oscillazione non varia in modo simmetrico -- si aggiunge una piccola asimmetria per il fatto che la cordicella viene costantemente accorciata però, rallentando la trazione, si riduce molto la asimmetria e i suoi effetti accumulati.

    Notiamo qui che l'invariante adiabatico E/ν ha le stesse dimensioni di joule-sec (cioè la stessa combinazione di quantità misurabili) della elusiva costante di Planck h.

    Gli invarianti adiabatici si ritrovano in tutti i tipi di moto periodico, compreso il moto kepleriano, che è stato preso come modello per il moto dell'elettrone attorno al nucleo. Alcuni fisici, in particolare Paul Ehrenfest, ipotizzarono che forse le orbite degli elettroni erano stabili quando l'invariante adiabatico I del loro moto corrispondeva ad h volte un certo numero intero. Per le orbite circolari in un atomo, esisteva soltanto un invariante adiabatico I, e consentendogli di assumere soltanto i valori I=nh con n=1,2,3... si ottenevano orbite con energie che si accordavano esattamente con lo spettro dell'idrogeno di Balmer.

    Alla fine risultò che la quantizzazione del momento angolare, piuttosto che quella di I, consentiva una migliore comprensione qualitativa degli atomi con più di un elettrone. Tutto questo viene discusso nella sezione successiva.