Assenza di pesoUn astronauta in orbita bassa attorno alla Terra si muove (approssimativamente) su una grande circonferenza che gira tutt'intorno alla Terra. L'accelerazione richiesta per un tale moto è fornita dalla gravità mg(RT/r)2= mv2/r dove il peso dell'astronauta che, sulla superficie terrestre a r = RT è pari a mg, è stato riaggiustato nel primo membro dell'equazione per una distanza maggiore di RT. Questa è naturalmente la stessa equazione che abbiamo usato per dimostrare lo studio di Newton sulla gravità. Tuttavia, può anche essere scritta mg (r/RT)2 – mv2/r = 0 Essa può essere interpretata affermando che, nel sistema di riferimento dell'astronauta, tutti i corpi sono soggetti a due forze, la gravità e la forza centrifuga, e queste due si equilibrano perfettamente tra loro, dando zero come somma. Si dice talvolta che gli astronauti nello spazio sono in un ambiente di "gravità zero", ma in realtà essi si trovano ancora pesantemente sotto l'influenza della gravità terrestre. È vero, un astronauta non nota alcuna tendenza a cadere verso la Terra, ma il motivo è un altro e può essere spiegato in uno di questi due modi:
Simulazione dell'assenza di peso in un aeroplanoChe cosa succederebbe se l'astronave non percorresse un'orbita circolare ma (diciamo) ellittica? Non farebbe alcuna differenza. Se la forza di gravità a una distanza r è
allora l'equazione del moto di un oggetto sottoposto alla sola forza F è
L'accelerazione a è quella percepita da un veicolo spaziale in orbita, dal punto di vista del sistema di riferimento fisso, solidale con la Terra. In un'orbita circolare di raggio r, l'accelerazione è pari a v2/r, mentre in un'orbita ellittica potrebbe avere una grandezza diversa e una direzione diversa, che potrebbero essere comunque calcolate. La cosa importante è di notare qui che un astronauta all'interno di un veicolo spaziale è soggetto alla stessa gravità e quindi partecipa della stessa accelerazione del veicolo spaziale. Osservando il moto dell'astronauta nel riferimento solidale con il veicolo spaziale, l'astronauta non è attratto verso il pavimento dell'abitacolo o verso qualche altra direzione, e quindi ha l'impressione che la gravità sia stata eliminata. Supponiamo invece che l'astronauta si trovi all'interno di una cabina in caduta libera (per esempio di un ascensore in cui si siano rotti i cavi), vicino alla superficie terrestre. Allora, anche in questo caso
ma poiché r è molto prossimo a RT, possiamo porre il rapporto uguale a 1 e scrivere semplicemente
La cabina cade con una accelerazione g, ma anche il passeggero cade con la stessa accelerazione, per cui, anche in questo caso, non c'è alcuna forza che spinga il passeggero verso il pavimento della cabina. Riferendosi alla cabina circostante, il passeggero avrà ancora l'illusione che la gravità non esista. Non farebbe alcuna differenza se la cabina partisse con una velocità costante -- per esempio, con una velocità iniziale u verso l'alto e con una velocità iniziale w in direzione orizzontale -- poiché nessuna di queste due influenzerebbe le forze e le accelerazioni. La cabina e il passeggero avrebbero ancora entrambi una accelerazione verso il basso pari ad a=g, creando l'illusione di assenza di gravità. Se si effettuasse questo esperimento nella realtà, l'illusione finirebbe e la cabina rapidamente si sfracellerebbe al contatto del suolo. Inoltre, la resistenza dell'aria ridurrebbe presto l'accelerazione della cabina a un valore inferiore a g. Il passeggero all'interno, ancora soggetto ad a=g, andrebbe giù più rapidamente della cabina, e in tale situazione, nel riferimento della cabina, sembrerebbe che la gravità fosse parzialmente tornata. Tuttavia, un esperimento simile può essere effettuato senza rischi a bordo di un aereo che voli ad alta quota e che possa vincere la resistenza dell'aria con la potenza dei suoi motori. Seguendo una traiettoria parabolica ben calcolata, simile a quella di un proiettile soggetto alla sola forza di gravità, un tale aereo può simulare -- per un tempo limitato -- una situazione di "gravità zero" all'interno della carlinga. La NASA ha effettivamente eseguito un tale esperimento con l'aereo KC-135, un quadrigetto soprannominato "La Cometa del Vomito" poiché il rapido passaggio a gravità zero fa venire a molti passeggeri il mal d'aria. L'aeroplano può riprodurre temporaneamente un ambiente di assenza di gravità all'interno della carlinga, e viene utilizzato per l'addestramento degli astronauti e per brevi esperimenti su fenomeni a gravità zero. L'interno della carlinga è completamente imbottito, e l'illusione di assenza di gravità può essere mantenuta per circa 20-30 secondi. Per vedere fotografie e altri dettagli, si può fare clic qui.
Nel film di fantascienza "2001: Odissea nello spazio" si vede una stazione spaziale rotante, la cui rotazione fornisce all'equipaggio una "gravità artificiale". Ha una struttura a forma di ruota, con dei corridoi radiali che collegano la ruota con l'ambiente situato al centro (ved. disegno). Questo ambiente al centro è dove avviene il trasferimento tra la stazione e l'astronave in visita. Si può fare clic qui per dettagli su questo tipo di progetto. A causa della rotazione, viene generata una sorta di gravità, in cui il "basso" è quello diretto verso l'esterno della ruota (Larry Niven ha esteso tale nozione in una fantasiosa novella di fantascienza, intitolata "Ringworld" -- "Un mondo ad anello" -- e altre successive). Quando si voglia calcolare questo effetto è più semplice usare il sistema di riferimento della stazione spaziale e aggiungere la forza centrifuga e le altre forze presenti su di essa. Tuttavia, quando ci si muove in questo ambiente in rotazione, specialmente andando su e giù per i corridoi radiali, si incontra un'altra forza, che ha preso il nome dal francese Gaspard Gustave de Coriolis (1792-1843). 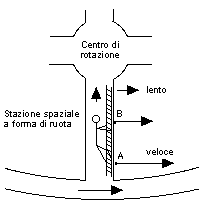
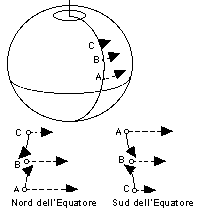
Immaginiamo un astronauta che si muova lungo uno di questi corridoi, diciamo dal punto A al punto B, nel disegno a fianco -- probabilmente salendo su una scaletta, poiché un tale tipo di moto si compie contro la "gravità artificiale" della stazione spaziale. In ogni punto, visto nel sistema di riferimento del mondo esterno, anche l'astronauta sta ruotando attorno all'asse della stazione. In entrambi i punti A e B, la rotazione avviene nello stesso verso, ma in B è più lenta, poiché questo punto è più vicino all'asse di rotazione e quindi compie una circonferenza più stretta. Nel punto B che cosa ne è della maggiore velocità che l'astronauta aveva in A? Secondo la prima legge di Newton, applicata approssimativamente, l'astronauta tenderebbe a mantenere la velocità eccedente e sarebbe quindi spinto contro la parete laterale del corridoio (direzione delle frecce). Questa spinta è la forza di Coriolis. Quando il moto avviene in verso opposto, da B ad A, il verso della forza è . . . lo stesso o invertito? Provate a ricavarlo da voi! L'acqua che scorre nello scarico del lavandinoDi tanto in tanto si sente dire che l'acqua che scorre nello scarico del lavandino ruota in verso opposto a nord e a sud dell'equatore. Il principio fisico è corretto, ma l'effetto pratico è così microscopico che è piuttosto improbabile riuscire a osservarlo nel lavandino del bagno. D'altra parte, questo stesso effetto è molto importante nella rotazione su larga scala dell'atmosfera, negli uragani, nei tifoni e nelle ordinarie configurazioni meteorologiche. |