(9b) L'ombra della Terra

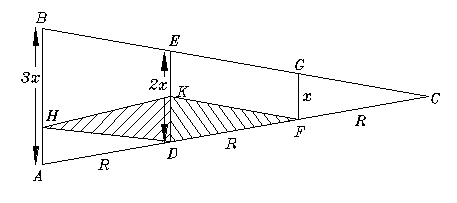
  In un'eclisse lunare, il diametro dell'ombra della Terra è il doppio del diametro lunare, per cui il diametro del globo terrestre è (molto prossimo a) tre volte il diametro della Luna -- non il doppio, come verrebbe da pensare. Ecco il perché.

 Il Sole non è una sorgente luminosa puntiforme ma una sorgente estesa: il suo disco copre una superficie circolare di cielo, con un diametro di circa 0,5°. Questo fatto rende l'ombra della Terra non cilindrica, cioè con una lunghezza infinita senza restringimenti, ma a forma di cono con un angolo di apertura di 0,5° dal suo vertice C (ved. disegno). AB rappresenta nella figura il diametro della Terra, e le direzioni AC e BC rappresentano i raggi provenienti dai bordi opposti del disco solare, raggi le cui direzioni formano tra loro un angolo di 0,5°.

 Se x è il diametro della Luna e R la sua distanza, allora secondo Aristarco il diametro ED dell'ombra alla distanza R è uguale a 2x (in realtà 2,5x è un valore più accurato). Aggiungiamo al disegno i punti H e K così che HA = KD = x.

 Il diametro della Luna, come è visto dal punto H, è KD = x, e poiché il disco apparente della Luna nel cielo ha circa lo stesso diametro di quello del Sole, l'angolo (tratteggiato) KHD deve anch'esso essere uguale a 0,5°. Prolunghiamo ora la linea AD = R di una ulteriore quantità R, fino al punto F. Allora i due triangoli tratteggiati HKD e KFD saranno congruenti (stessa forma e stesse dimensioni) e avranno l'angolo in H e l'angolo in F uguale all'angolo in C, pari a 0,5°. Si può ora dimostrare che anche i triangoli GFC e AHD sono congruenti con i due tratteggiati.

Ne segue quindi che AC = 3R, e da una semplice proporzione (ved. disegno) AB = 3x.