El Núcleo Atómico.La ley de Planck describe la manera en que una masa de materia caliente irradia energía. Para obtener información acerca de los átomos mismos, sin embargo, se necesita entender la estructura intrincada de niveles de energía, tal y como se deduce de los espectros atómicos. ¿Cómo eran los átomos y qué determinaba esos niveles?
J.J. Thomson, el descubridor del electrón, pensó que el átomo pudiera consistir en una masa cargada positivamente, dentro de la cual electrones negativos estaban encapsulados ("como pasas en un pudín"), y otros especulaban respecto a los detalles de dicho modelo. Visto desde el exterior, las fuerzas eléctricas de cargas opuestas positivas y negativas podrían balancearse unas con otras, de manera que desde lejos, cualquier átomo podría parecer neutro eléctricamente. Sin embargo, se esperaba que los electrones oscilen alrededor de sus puntos de equilibrio, e irradiar con las frecuencias características de su oscilación, de acuerdo a la teoría de Hertz. La fórmula de Einstein
entonces sugería una asociación entre las frecuencias de oscilación y las energías irradiadas. Esta bonita imagen fue descompuesta debido a un experimento notable realizado en Manchester en 1909 por Ernest Rutherford, originario de Nueva Zelandia. Por ese tiempo era conocido que los elementos radiactivos pesados emitían "partículas alfa" (partículas α), iones rápidos de helio que carecían de sus dos electrones. Eso les dió una carga positiva de +2e, el doble de carga eléctrica de –e. Rutherford sabía cómo detectar tales iones de manera individual. En una oscuridad total, si se les permitía golpear una pantalla fluorescente especialmente preparada, el destello que producían era suficientemente brillante para poder verse por un ojo adaptado a la oscuridad, observando una pequeña parte de la pantalla a través de un microscopio. Se encontró que las partículas α tienen suficiente energía para penetrar una pequeña lámina de oro, y por lo tanto Rutherford puso a su asistente Hans Geiger (después asistido por Ernest Marsden) a examinar cómo el paso a través de tal lámina afectaba su movimiento. Con un átomo que se parece al propuesto por J.J. Thomson, los iones no sentirían fuerza eléctrica mientras estuvieran fuera del átomo de oro, en cuyo interior los efectos de cargas positivas y negativas se cancelaban. Si ellos pasaban a través de las orillas del átomo, los cálculos sugerían que la carga eléctrica positiva distribuída, podría deformar ligeramente su camino.
Lo que vieron Geiger y Marsden, sin embargo, era bastante diferente. La mayoría de las partículas α en realidad pasaban a través de la lámina con tan solo pequeñas deflecciones. Pero unas pocas eran dispersadas en grandes ángulos, de una manera que solo podía ser explicada asumiendo que la carga positiva del átomo de oro y la mayoría de su masa formaban una concentración tan pequeña como un punto. Fue solamente entonces cuando la partícula bombardeadora pudo acercarse tan cercamente que su repulsión eléctrica pudo desviarla en un gran ángulo o aún más, regresarlo. Los electrones se quedaron lejos afuera del núcleo, como planetas orbitando lejos del Sol, una representación de hecho sugerida por Hantaro Nagaoka en Japón.
Cada uno de estos dos movimientos (independientes) es equivalente a una carga eléctrica oscilando hacia arriba y abajo alrededor de un punto de equilibrio. De acuerdo a las leyes de Maxwell y Hertz, sin embargo, a tal electrón se le espera que emita radiación electromagnética, con lo cual debería de reducir su energía. Debido a esto, a diferencia de los planetas del sistema solar, los electrones deberían irradiar rápidamente su energía y realizar un giro en espiral hacia adentro, hasta que lleguen al núcleo. Los átomos, sin embargo son (¡afortunadamente!) estables ¿cómo es esto?
Modelo del Átomo de Bohr.Los resultados de Balmer y Ritz parecían decir que los átomos tenían niveles de energía estables, y la fórmula de Einstein sugería que la energía a niveles atómicos parecía estar relacionada con la constante de Planck h, medida en joules-seg.Una cantidad medida en joules-seg era el momento angular. Esta es una propiedad mecánica (tal y como la energía lo es) de cualquier objeto rotatorio o colección de objetos, aún de la Tierra, el Sol o el sistema solar. Este mide la "cantidad de rotación" total, de acuerdo a la masa involucrada, su distancia promedio del eje de rotación, y por supuesto, su relación de rotación. Es una cantidad vectorial, su dirección sigue el eje de rotación. La rotación de la Tierra y el Sol, así como los movimientos orbitales de los planetas y las lunas, involucran momento angular. Un joven físico danés llamado Niels Bohr, quien llegó a Inglaterra en 1912 y terminó trabajando con Rutherford en la Universidad de Cambridge, estudió el momento angular de un electrón orbitando un núcleo. Fue conjeturado entonces que una vez que las dimensiones del movimiento se encogen a una escala atómica, las leyes de Newton se iban modificando gradualmente, permitiendo que los electrones tengan órbitas donde (por una razón tadavía desconocida) no se perdía energía al emitir ondas electromagnéticas. Borh fué un paso más lejos todavía: tal vez las órbitas eran estables cuando el momento angular del movimiento equivalía h veces algún número entero. En un sistema grande, este podía ser millones de veces más grande que h, de manera que la ley permitía momento angular (y energía) para cambiar casi continuamente. En la escala de un átomo de hidrógeno, sin embargo, las posibilidades eran pocas, las órbitas estables eran bastante distintas, así como sus niveles de energía.
Esto funcionaba de maravilla en órbitas circulares en un átomo de hidrógeno, y también daba un valor consistente con la constante de Rydberg. Permitiendo que el momento angular tomara valores de nh/2π con n=1,2,3... producía órbitas con energía que concordaban exactamente con el espectro de hidrógeno de Balmer (el factor 2π puede ser justificado). Un promisorio primer paso, pero, ¿como continuar desde aquí?
La sección de abajo es opcional. Esta representa una idea alterna, de unir niveles cuánticos con valores de invariantes adiabáticas del movimiento, las cuales también tienen unidades de joule-seg. Esto también condujo a niveles correctos de hidrógeno, pero ultimadamente se convirtió en un callejón cerrado. La razón principal para traer esto a colación es que mucho después, las invariantes adiabáticas se hicieron útiles en la física Newtoniana de los plasmas y las partículas con cargas atrapadas en un campo magnético (vea las referencias en el último párrafo que le llevará a una página web relacionada). Invariantes Adiabáticas.
Las leyes físicas, las básicas y aquellas derivadas de ellas, normalmente ofrecen enunciados precisos, cuantitativos, como F=ma, E=mc2, E= hν. Raramente se encuentra uno con una ley en la cual algo es aproximadamente cierto, pero no exactamente (aún cuando la aproximación pueda ser muy buena), por ejemplo, válida por un largo tiempo pero no por toda la eternidad. La invarianza adiabática es de este tipo.
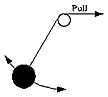
Imagine un péndulo formado por una pesa atada a una cuerda, oscilando hacia atrás y hacia adelante bajo la influencia de la gravedad. En cada oscilación, al descender hacia la parte más baja de su giro, gana energía cinética, y luego de haber pasado por la parte más baja, reduce su velocidad de nuevo, para detenerse momentáneamente en la parte superior de cada giro. En la ausencia de fricción y de la resistencia del aire, se espera que la energía total E ( cinética + potencial ) permanezca sin cambio, y que la frecuencia ν y el período T=1/ν de la oscilación permanezca constante también. Si la cuerda comienza en una polea (vea dibujo) y es lentamente subida, la longitud del péndulo decrecerá gradualmente, y dado que un péndulo más corto tiene una frecuencia ν más grande y un período T más corto, estas cantidades también se espera que cambien. Pero la energía E crece también, debido a que se está realizando un trabajo adicional contra la fuerza que estira la cuerda, de manera que el giro se hace más vigoroso. Suponga que la cuerda es jalada hasta que su longitud se reduce en una cierta fracción digamos, a la mitad. Se puede demostrar que el cambio en la relación E/ν puede ser realizado tan pequeño como deseemos haciendo el jalón suficientemente lento. La relación no es una constante real del movimiento, o "invariante" (como la energía en un péndulo sin perturbaciones), sino una aproximación, una "invariante adiabática". La falta de constancia puede ser atribuída al hecho de que la tensión en la cuerda en cualquier giro no varía simétricamente; una pequeña asimetría se agrega por el hecho de que la cuerda es continuamente recortada, pero disminuyendo el jalón reduce grandemente la asimetría y sus efectos acumulados. Nótese aquí que la invariante adiabática E/ν tiene las mismas dimensiones de joule-seg (por ejemplo la misma combinación de cantidades medibles, también llamada "acción") al igual que la elusiva constante de Planck h. Las invariantes adiabáticas ocurren en todo tipo de movimientos periódicos, incluyendo el movimiento de Kepler, el cual fue tomado como modelo del movimiento de un electrón alrededor del núcleo. Algunos físicos, especialmente Paul Ehrenfest, supuso que tal vez las órbitas de los electrones eran estables cunado la invariante adiabática I de su movimiento equivalía a h veces algún número entero. Para las órbitas circulares en un átomo, solo una invariante adiabática I existía, y permitiéndole que solo tome los valores I=nh con n=1,2,3... el cual daba órbitas con energías que concordaban exactamente con el espectro de hidrógeno de Balmer. Al final ocurrió que la cuantificación del momento angular, en lugar de la cuantificación de I, daba un mejor entendimiento de los átomos de más de un electrón. Esto se discute en la siguiente sección. Las invariantes adiabáticas de nuevo atrajeron la atención en los años 50īs, en el estudio del movimiento de los iones y electrones en plasmas de gases rarificados. El plasma es un gas suficientemente caliente para contener una fracción apreciable de iones y electrones desprendidos, y si está bastantemente rarificado, como es el caso del plasma en la "magnetósfera" que rodea la Tierra, estas partículas se pueden mover de manera independiente durante largos tiempos antes de recombinarse. En la presencia de un campo magnético suficientemente fuerte, estas tienden a girar en espiral alrededor de las líneas del campo magnético,el cual es un movimiento periódico, con sus invariantes adiabáticas específicas (de hecho, existen bastantes periodicidades e invariantes). La conservación de esas invariantes se convirtió en algo escencial para atrapar las partículas en los campos magnéticos de la Tierra y otros planetas, y también para algunos fenómenos de plasma en el espacio y en el laboratorio. Pero esta aplicación de las invariantes era parte de la mecánica ("clásica") de Newton, sin involucrar la constante de Planck h pero describiendo el fenómeno en una escala mucho mayor que las dimensiones atómicas. Para saber más acerca de este campo de la investigación, vea la exposición " Exploración de la Magnetósfera de la Tierra", a cuyos archivos le llevará el vínculo anterior. |
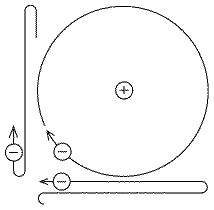Parecía como un sistema planetario en miniatura, con la atracción entre los núcleos positivos y electrones negativos haciendo las veces de la gravedad, una atracción que, al igual que la gravedad, decrece al cuadrado inverso de la distancia R, como 1 / R2. Un electrón mantenido de esta manera debe obedecer las leyes de Kepler, igual que un planeta atraído por la gravedad, y moverse en un círculo o elipse. Entonces, su movimiento puede ser visto como la suma total de dos oscilaciones perpendiculares, cada una logrando su máxima extensión en el momento que la otra pase por el punto medio (solo considere las "sombras" de el movimiento en los ejes X y Y, mostrados en el dibujo).
