Aceleración
Un objeto dejado caer comienza su caída muy lentamente, pero aumenta
su velocidad constantemente, acelera, con el tiempo. Galileo demostró
que (ignorando la resistencia del aire) los objetos ligeros y pesados aceleran
a la misma razón constante cuando caen, o sea, su velocidad
aumenta a una razón constante. La velocidad de una bola que cae
desde un lugar elevado aumenta cada segundo una cantidad constante, designada
normalmente por la letra g (de gravedad). En unidades modernas
(usando la convención del álgebra, en la que los símbolos
o los números que están al lado de otros se entiende que
se multiplican) su velocidad es
al comienzo -- 0 (cero)
después de 1 segundo -- g metros/segundo
(m/s)
después de 2 segundos -- 2g m/s
después de 3 segundos -- 3g m/s
y etc... Esto se modifica con la resistencia del aire, que se hace importante
a velocidades elevadas y, normalmente, fija una velocidad límite
a la velocidad de caída ("velocidad terminal"); mucho menor, por
ejemplo, para quien use un paracaídas que para quien no lo haga.
El número g está cercano a 10, con más precisión:
9.79 en el ecuador, 9.83 en el polo y valores intermedios entre ambos lugares,
y se conoce como "la aceleración debida a la gravedad". Si
la velocidad aumenta 9.81 m/s cada segundo (un valor medio bueno),
g
se dice que es igual a "9.81 metros por segundo por segundo" ó,
lo que es lo mismo, 9.81 m/s2.
Añadiendo una Velocidad Inicial
Considere que la bola tiene una velocidad inicial u hacia arriba
ó hacia abajo. Si las distancias hacia abajo
se eligen como positivas, la velocidad debida a la gravedad será
siempre positiva, mientras que u será positiva si
se dirige hacia abajo y negativa si lo hace hacia arriba.
Con esta cláusula, las observaciones indican que u
debe ser sumada en todas partes a la velocidad debida a la gravedad, hallando
la velocidad en segundos sucesivos (como en la lista superior)
u, u+g, u+2g, u+3g . . .
y, en general, después de t segundos
u + gt
(gt significa: "g veces t")
La Distancia Cubierta
La distancia cubierta por la bola puede parecer ser la misma que la cubierta
si la bola tiene una velocidad constante "media" v(media),
igual a la semi-suma de las velocidades de comienzo y final.
Para la bola descendente del ejemplo anterior, después de t
segundos será
v(media) = (1/2)[u + (u+gt)]
haciendo a la distancia cubierta
distancia = t v(media) = ut + (1/2) gt2
El Experimento de Galileo
El libro "The God Particle" de Leon Lederman, ganador del Premio Nobel,
y de Dick Teresi (un buen libro, si acepta su actitud irreverente y humor
hortera) nos dice como Galileo mostró que el movimiento descendente
de una esfera debido a la gravedad tiene una aceleración constante,
y que a partir del reposo (u = 0) cubre una distancia que
aumenta en proporción al cuadrado del tiempo transcurrido,
tal y como se muestra en la fórmula superior.
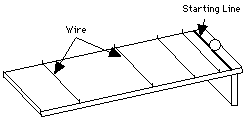
Dado que una caída vertical era muy rápida para que Galileo
la midiera con precisión, la ralentizó haciendo que la esfera
rodase por un tablero inclinado. A través del tablero, a lo largo
de su superficie, engarzó una serie de alambres horizontales tirantes,
haciendo que sonara un clic siempre la bola saltaba sobre unos de ellos.
Galileo movió luego los alambres hacia arriba y abajo del tablero
hasta que los clics sonaron espaciados uniformemente.
Si ahora la aceleración es a (mucho menor que g)
y el tiempo t se mide en clics, mediante la fórmula
superior, comenzando con la bola en reposo (u= 0) se obtiene
la distancia cubierta S
Después de un clic S = (a/2) 12
= a/ 2
Después de dos S = (a/2)
22 = 2a
Después de tres S = (a/2)
32 = 4.5 a
y así sucesivamente. La proporción entre las distancias deberá
ser la de los cuadrados 1, 4, 9, 16, 25. . . y eso fue lo que Galileo confirmó.
Si convertimos los clics en segundos, tenemos en cuenta el ángulo
del tablero y también el hecho de que la bola rodaba (una
teoría que no estaba disponible en los días de Galileo),
podremos calcular, en principio,
g a partir de a.
Cataratas y Pelotas de Béisbol
Además, si al comienzo la bola se mueve con una velocidad horizontal
w, su movimiento horizontal continúa sin ningún
impedimento, avanzando una distancia w cada segundo, aunque
la bola esté cayendo (ignorando la resistencia del aire). Los dos
movimientos tienen lugar simultáneamente, haciendo que la bola siga
una curva, que gradualmente se hace más pronunciada debido a que
la velocidad de caída se va incrementando, mientras que la horizontal
no. Es así como se mueven las gotas en una catarata, lo que proporciona
a la sección transversal su forma característica (izquierda).

La escena que se ve continuamente en las películas de dibujos
animados de "El Correcaminos", en la que Wily Coyote corre más allá
del borde del acantilado, suspendiéndose en el espacio (hasta que
se da cuenta) y luego cae a plomo es una ficción de la imaginación,
totalmente contraria a las leyes de la física. En la realidad tienen
lugar los dos movimientos simultáneamente. De igual modo, una bala
disparada por un rifle sobre una diana comienza a caer desde el mismo momento
en que abandona la boca del rifle. Es necesario ajustar el visor del rifle
para la distancia apuntando hacia un punto por encima del blanco, calculado
a fin de que, a la distancia apropiada, con la caída, la bala la
dirija hacia abajo, hacia la diana.
Para una piedra arrojada hacia arriba, u es negativa y
estará a una distancia vertical indeterminada sobre el punto de
lanzamiento. En este caso, haga U = -u un número
positivo. Luego después de t segundos
velocidad = (-U + gt) m/s
Al principio t es pequeño y la velocidad es negativa,
mostrando a la piedra moverse hacia arriba. En el momento que
gt = U
la suma es cero y durante un breve instante la piedra está en
descanso, en la cúspide de su trayectoria. En ese momento
t = U/g
y si el valor se usa en la fórmula para la distancia, se obtiene
la altura a la cual ocurre. Y, en conclusión, si se añade
a este movimiento una velocidad constante horizontal w, se
deducirá el movimiento de una pelota de béisbol o el de una
bala de cañón.
Respecto a la resistencia del aire
Las fórmulas de arriba solo se cumplen para balas de cañón
ideales que no experimentan resistencia del aire. En la práctica,
esta resistencia modifica el movimiento y debe de tenerse en cuenta, especialmente
en la caída de objetos ligeros, como puede ser una pluma. Una demostración
científica popular durante siglos ha sido la de una moneda y una
pluma cayendo simultáneamente en el interior de un tubo de cristal,
al cual se le ha hecho el vacío: siempre se les ve a las dos caer
con la misma velocidad.
Una demostración similar fue hecha también en la superficie
de la Luna por uno de los astronautas del Apolo. No solo la Luna no tiene
atmósfera, sino que su gravedad es varias veces más débil,
haciendo que la caída sea más lenta y más fácil
de observar. El astronauta dejó caer la moneda y la pluma delante
de una cámara de TV y su audiencia en la Tierra que estaban viendo
la TV, observó a las dos cayendo juntas.
Aunque, como anécdota, el astronauta probó primero su
experimento fuera de la visión de la cámara, para estar seguro
de que funcionaba. |


