Nota: En esta lección, como en la precedente, todos los vectores serán subrayados.

(23a) Marcos de Referencia: La Fuerza Centrífuga

El alumno, madrugando para su examen, estaba confundido..."Centrífuga, centrípeta", decía, con su barbilla apoyada en su puño. "Parar un planeta en su vuelo, privarlo de su fuerza centrífuga, ¿y luego que ocurre? ¡Le queda su fuerza centrípeta y cae hacia el Sol! Y esto---!"

H.G.Wells, La Estrella

Ahora regresemos al movimiento circular.

La Fuerza Centrífuga

El movimiento circular es un movimiento acelerado. Por consiguiente, si lo estudiamos en el marco de referencia giratorio, podemos prever que aparecerán fuerzas de inercia, como las abordadas en la sección anterior.

Suponga a una persona sentada en un autobús, moviéndose en línea recta con velocidad constante v. Como antes, las fuerzas involucradas son el peso del pasajero F₁ y la fuerza de reacción del asiento F₂y en ausencia de aceleración, las dos se cancelan:

F₁+ F₂ = 0

De repente el autobús hace un giro brusco, siguiendo parte del círculo de radio r. Si el cuerpo del pasajero sigue en el asiento como antes, se añadirá una fuerza extra, para evitar que continúe en línea recta (su tendencia natural). Si r_u en un vector unidad (los vectores unidad se explicaron en la sección anterior ) dirigido hacia fuera del centro de rotación, a lo largo del radio r, la fuerza F₂ ejercida por el asiento debe incrementarse para proporcionar la fuerza centrípeta -(mv²/r)r_u que hace que el pasajero siga el movimiento del autobús:

F₁+ F₂ = - (mv²/r) r_u

El autobús y el asiento obligan al cuerpo del pasajero a seguir parte del círculo y para conseguir esto deberá de tirar de él hacia el centro. Para permanecer en el sitio (o sea, equilibrar la ecuación anterior), F₂ debe de incrementarse con una fuerza adicional en la dirección de -r_u, hacia el centro de la curva.

¿Cómo se ve el mismo caso desde el marco del autobús? Sumando (mv²/r)r_u a ambos lados de la ecuación da, de forma similar a como lo hizo anteriormente

F₁+ F₂ + (mv²/r) r_u = 0

Se consigue el equilibrio y el pasajero continúa en su sitio, si se cumple la ecuación anterior. Esto se puede ver como el equilibrio entre tres fuerzas-- F₁,F₂ y la fuerza centrífuga (mv²/r)r_u dirigida a lo largo de r_u, radialmente hacia fuera.

Se puede fácilmente generalizar a cualquier marco de referencia moviéndose circularmente:

Existe el equilibrio en el marco giratorio si todas las fuerzas se equilibran, incluida la fuerza "centrífuga" de inercia (mv²/r)r_u.

Ejemplos

Cuando se calculan los movimientos de los océanos y la atmósfera, es más fácil usar puntos de referencia sobre la Tierra giratoria y añadir una fuerza centrífuga a todas las ecuaciones. Esta es una razón del porqué la aceleración observada g debida a la gravedad tiene un valor medio de 9.81: en el ecuador, la fuerza centrífuga debe restarse de la fuerza de la gravedad, mientras que en el polo no existe fuerza centrífuga. Las observaciones de g dan valores desde 9.78 en el ecuador hasta 9.83 en los polos, pero la fuerza centrifuga es la responsable solo de parte de esa diferencia. El resto se origina porque la Tierra no es una esfera perfecta: la fuerza centrífuga de su rotación causa que en el ecuador se abulte, haciendo que la superficie allí esté más distante del centro de la Tierra y esto debilita la atracción gravitacional.

eje de rotación

Otro ejemplo es el "looping" de algunas montañas rusas en los parques de atracciones. Allí la pista desciende en una larga rampa y luego, en el fondo, gira en un círculo completo (dibujo) antes de nivelarse de nuevo. En el punto señalado como "A" los pasajeros están cabeza abajo un breve momento, pero ninguno cae. ¿Como es posible? Y (en ausencia de fricción), ¿cual es la altura mínima h, del punto de arranque S encima de A necesario para asegurar que el coche pasa con seguridad por A ?
Esto se resuelve fácilmente en el marco del coche de la montaña rusa en movimiento. En ese marco, las fuerzas sobre el coche en la parte superior del lazo son

El peso -mg r_u (hacia abajo, a lo largo de -r_u en ese punto.)
La fuerza centrífuga (mv²/r) r_u, y
La fuerza F₂ ejercida por los raíles.

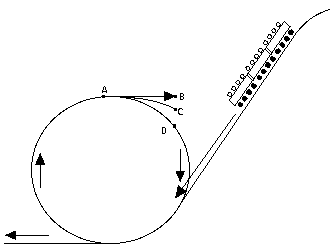
El coche apenas logrará pasar el punto A si la gravedad y la fuerza centrífuga son exactamente iguales, así los raíles no necesitan ejercer un fuerza extra:

-mg r_u + (mv²/r) r_u = 0

Los dos vectores están a lo largo de r_u (con signos dando su dirección), así todo se reduce a una ecuación entre números ordinarios:

-mg + mv²/r = 0

Suponga ahora que el coche bajó desde una altura h sobre el punto más alto del lazo. Ha

perdido energía potencial mgh, y
ganado energía cinética mv²/2

así, de la conservación de energía

mgh + mv²/2 ó 2mgh = mv²

Substituyendo

-mg + 2mgh/r = 0

Dividido por mg, sumando +1 a ambos lados:

2h/r = 1 luego multiplique por r/2 para obtener h: h = r/2

El coche deberá comenzar la bajada como mínimo a medio radio del lazo sobre A.

Pulse aquí para ver una sección opcional tratando el mismo problema usando la fuerza centrípeta.

Exploración Adicional:

Para una demostración del "looping" con un auto de juguete "hot wheels" pulse aquí.
Un lugar sobre montañas rusas, el más grande, más alto, el que tiene más loops (8) y el de mayor loop ("Moonsault Scramble" en Japón, su foto al comienzo de esta página ) pulse aquí.

Página principal en Español (índice)

Linea del Tiempo Glosario .

Opcional: (23b) El Bucle

Próxima Etapa: #24 Marcos de Referencia Giratorios

Author and Curator: Dr. David P. Stern
Messages to Dr.Stern: stargaze("at" symbol)phy6.org (English, please) .

Spanish translation by J. Méndez

Last updated 13 December 2001