Además de la Luna, la Tierra tiene ahora muchos satélites
artificiales, usados por nosotros, los terrícolas, con propósitos
diversos. Los cálculos aplicados por Newton a la Luna pueden usarse
para los satélites.
Velocidad OrbitalSuponga que la Tierra fuese una esfera perfecta de radio1 RE = 6 317 000 metros y no tuviera atmósfera. En principio, un satélite podría orbitar justo sobre su superficie. La Tierra lo atraerá con una fuerza F = mg y debido a la dirección de esa fuerza, cualquier aceleración será también en la dirección arriba-abajo.Si el satélite está en una órbita circular estable y su velocidad es V, luego F proporciona la cantidad justa de atracción para mantener el movimiento. Lo que significa mg = F = mV2/RE Dividiendo ambos lados por m se ve que la masa del satélite no importa, y queda V2/RE = g Multiplicando ambos lados por RE: da V2 = (g) (RE) = (9.81) (6 371 000) = 62 499 510 (m/s2) V = 7905. 66 m/s = 7.90566 km/s = Vo 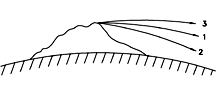
Esta es la velocidad requerida por el satélite para permanecer en su órbita ("1" en el dibujo). Cualquier disminució, pierde altitud y choca contra la Tierra ("2"); cualquier incremento, sube a gran distancia ("3"). Para comparación, un avión comercial vuela a unos 250 m/s, una bala de rifle a unos 600 m/s. Necesitamos de nuevo una notación para la raíz cuadrada. Como el lenguaje HTML no dispone de una, usamos la notación SQRT que encontramos en algunos lenguajes de computación. La raíz cuadrada de 2, por ejemplo, puede escribirse SQRT(2) = 1. 41412. . . Si la velocidad V de nuestro satélite es solo un poco mayor que Vo, curva "3", será parte de una elipse kepleriana y retornará de nuevo a la Tierra. Si, no obstante, V es mayor que 1. 4142. . .veces Vo el satélite adquiere velocidad de escape y nunca volverá: esto ocurre a unos 11.2 km/s. 3ª Ley de Kepler para Satélites TerrestresLa velocidad de una órbita circular de la Tierra a cualquier otra distancia r se calcula de forma similar, pero se debe tener en cuenta que la fuerza de gravedad es más débil a mayores distancias, por un factor (RE/r)2. Entonces obtenemosV2/r = g (RE r)2 = g RE2/r2 hagamos a T ser el período orbital en segundos. Luego (como se dijo antes), la distancia 2 πr cubre una órbita igual a VT |