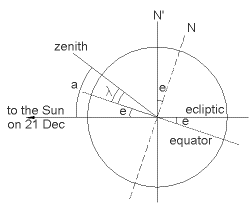
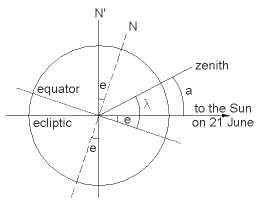
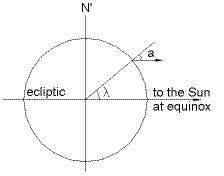
| Para cualquier otra fecha, existen tablas de
navegación que indican los ángulos apropiados (menores
de 23.5º) que deben ser sumados o restados. También
proveen de fórmulas para deducir la altura del Sol desde
observaciones hechas a otras horas. Al igual que
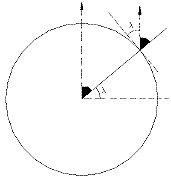
con la estrella Polar, mejor que medir el ángulo a
desde el cenit, ¡que no está marcado en el cielo!, es
más sencillo medir el ángulo (90°-a) desde el
horizonte, que en la mar, habitualmente, está claramente
definido. Tales observaciones, conocidas como "medir
la altura del Sol", se hacen con un instrumento
llamado sextante. Tiene una escala deslizante que
cubre 1/6 de un círculo (de ahí su nombre) y un espejo
anexo pivotante, que permite una vista dividida: el
piloto, moviendo la escala, trae al Sol y al horizonte
simultáneamente a la vista y luego lee, por fuera del
sextante, el ángulo entre ellos.
Longitud
En la época de los grandes navegantes, Colón,
Magallanes, Drake, Frobisher, Bering y otros, localizar
su latitud era una tarea fácil. Los capitanes sabían
como usar el Sol del mediodía y antes de que se
inventara el sextante, se usaba un instrumento menos
preciso llamado alidada.
La longitud era un hueso más duro de roer. En
principio, todo lo que se necesita es un reloj de
precisión, ajustado a la hora de Greenwich. Cuando el
Sol "pasa el meridiano" al mediodía, solo
necesitamos comprobar el reloj: si a la hora de Greenwich
son las 3 p.m. (15:00), sabemos que 3 horas atrás era
mediodía en Greenwich y, por lo tanto, estamos a una
longitud de 15° x 3 = 45º oeste.
Sin embargo, los relojes de precisión requieren una
tecnología bastante sofisticada. Los relojes de péndulo
pueden medir el tiempo con precisión en tierra firme,
pero el balanceo y cuchareo de un barco los hacen
inservibles para su uso en la mar.
Los relojes sin péndulo, como los de pulsera antes de
ser electrónicos, usan un volante de inercia, una
pequeña rueda flotante girando adelante y atrás en un
ángulo pequeño. Un muelle espiral liso enrollado
alrededor de su eje hace retornar al volante a su
posición original. El periodo de cada oscilación está
así determinado por la tensión del muelle y por la masa
del volante y puede entonces reemplazar a la oscilación
del péndulo para controlar el movimiento de las
manecillas del reloj.
La gravedad no juega aquí ningún papel y los
movimientos del barco también tienen muy poco efecto;
como se discutirá en una sección posterior, un sistema
vagamente similar fue usado para "pesar" a los
astronautas en el medio ingrávido de una estación
orbital. Para la navegación, sin embargo, el reloj debe
ser muy preciso, lo que es difícil de conseguir:
la fricción debe ser mínima y así deben ser también
los cambios en las dimensiones del volante y en las
propiedades del muelle debidos a las modificaciones de
temperatura y otros factores.
En los siglos XVII y XVIII, cuando los navíos de
Inglaterra, España, Francia y Holanda intentan dominar
los mares, el "problema de la longitud" cobra
gran importancia estratégica y ocupa a algunas de las
mejores mentes científicas. En 1714 Inglaterra anuncia
un premio de 20,000 libras, una suma inmensa en aquellos
días, por una solución fiable y John Harrison, un
relojero británico, consume décadas intentando
conseguirla. Sus dos primeros "cronómetros" de
1735 y 1739, aunque fiables, eran piezas de maquinaria
delicadas y voluminosas; han sido restaurados y están
expuestas al público en el Real Observatorio
Astronómico de Greenwich. Solo su 4º instrumento,
probado en 1761, demostró ser satisfactorio y fueron
necesarios algunos años más antes de recibir el
premio.
Un sitio amplio y delicioso en la web con la historia
del "problema de longitud" de Jonathan
Medwin, se puede encontrar aquí.
Otra fuente recomendada es el libro Longitude de
Dava Sobel. .
Robert Wood fue un profesor de
la Universidad Johns Hopkins durante la primera mitad del
siglo XX distinguido por su trabajo sobre óptica física
y también por su sentido del humor y su amor a los
trucos malévolos.
En septiembre de 1917, Wood y
algunos colegas embarcaron para Europa a bordo del vapor Adriatic,
para ayudar a los aliados de los Estados Unidos a usar la
ciencia en los combates de la Primera Guerra Mundial.
Para evitar que los submarinos alemanes interceptaran el
barco, su localización fue mantenida en secreto a todo
el mundo, incluídos los pasajeros.
Lo que sigue son las propias
notas de Wood, reproducidas en "DoctorWood", de
William Seabrook (1940). El libro ya no se edita, pero
sigue siendo apropiado para su lectura (si se puede
encontrar) por su gran contenido de historias, de las
cuales esta es un buen ejemplo.
- "Navegamos noche tras
noche, el tiempo era cada vez más frío, y la
Estrella Polar escalaba hacia el zénit. Una
tarde se le ocurrió a Colpitts [uno de los
científicos en la travesía] que era la
noche del equinocio de otoño, en la cual ambas
longitud y latitud pueden ser calculadas por la
elevación de la Estrella Polar y el momento de
la puesta del sol [6 horas después de
mediodía]. Hice un cuadrante con dos
palitos de madera y un portaángulos. Observando
un palito sobre el horizonte y el otro sobre la
estrella, determiné su elevación, dada la cual
Colpitts, que había medido el tiempo desde la
puesta, calculó nuestra posición en unos pocos
minutos. Esta noticia se extendió rápidamente,
poniendo frenéticos a los oficiales del barco,
porque toda información relacionada con el curso
que estábamos siguiendo era mortalmente secreta.
A la mañana siguiente descubrimos que los
oficiales del barco habían ajustado todos los
relojes a disposición de los pasajeros
adelantándolos en tres cuartos de hora, para
confundir y despistar a los científicos que iban
a bordo."
Cuando entra en escena la radio, a
comienzos del siglo XX, la fiabilidad de los cronómetros
se hace menos crítica, porque la radiodifusión de las
señales horarias permite que los relojes del buque se
ajusten periódicamente. Pero hasta entonces los
cronómetros fueron esenciales para una navegación
fiable, como lo ilustra la historia siguiente.
En 1893 el explorador noruego
Fridtjof Nansen sale hacia el polo norte (situado en el
helado Océano ártico), en un buque especialmente
reforzado, el "Fram". Habiendo estudiado las
corrientes del Océano ártico, Nansen permite al
"Fram" congelarse en el hielo polar, sobre el
que es arrastrado lentamente sobre el agua. Cerca de dos
años más tarde, dándose cuenta de que el
"Fram" pasaría un poco alejado del polo,
Nansen (que estaba preparado para esa eventualidad)
abandona el barco con su colega Johansen e intenta
alcanzar el polo con trineos sobre el hielo. A unas 400
millas del polo deben dar la vuelta: hibernan en una isla
desolada, en un cabaña que construyen ellos mismos con
piedras y pieles de morsa y a la primavera siguiente se
dirigen a las Islas Svalbard (Spitzbergen).
Habían estado más de un año en la
inmensidad del hielo, completamente fuera de contacto,
pero siempre supieron exactamente donde estaban, porque
cada uno llevaba un cronometro de cuerda. Pero les acecha
el desastre. En un momento de distracción, ambos olvidan
dar cuerda a sus cronómetros y se les paran. De repente,
¡estaban perdidos!. Basándose en sus últimas
posiciones registradas, hacen conjeturas y ajustan sus
relojes, pero el resto del viaje estuvo sembrado de
incertidumbre. Afortunadamente, no tienen que ir muy
lejos porque, como el azar lo había dispuesto así,
encuentran una expedición británica al ártico que los
lleva a casa. El "Fram" se libera al borde del
hielo casi al mismo tiempo; ahora está en exhibición
pública en Oslo.
|