Centro de GravedadLa mayoría de la gente tiene, como mínimo, una noción intuitiva del centro de gravedad (CG) de un objeto: es el punto en el cual el objeto puede estar equilibrado. Agarre una escoba por un extremo y el otro extremo inténtelo dejar caer, agárrela por su centro de gravedad, y permanecerá equilibrada, sin que ningún extremo se eleve.Si ha probado a equilibrar una silla ó una escoba sobre la palma
de su mano, sabe que el truco es colocar su mano bajo el centro de gravedad.
Como su mano no está en el CG sino debajo, puede moverse perfectamente para mantener esta posición estratégica.
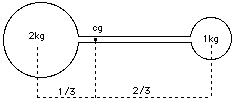
Existe un definición matemática precisa, no tiene nada que ver con la gravedad, por lo cual muchos científicos e ingenieros prefieren el término centro de masa. Sin embargo, se sale del tema principal y, por lo tanto, no nos molestaremos con él ahora. Un bastón ligero con dos bolas de igual peso en sus extremos tiene, obviamente, su CG en el medio. Cuando una bola tiene un peso doble de la otra, el CG divide la distancia entre ellas con una relación 1:2, de forma que estará más cerca de la masa más pesada (vea el dibujo). De modo semejante para otras relaciones. Bolas que se empujan mutuamente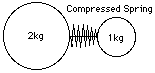 Imagínese
ahora, por ejemplo, que en el bastón anterior las dos bolas tienen
un muelle entre ellas. Aunque las bolas están separadas, se puede
hablar de su CG común, en la línea que conecta sus centros,
a 1/3 de la distancia del centro de la bola mayor.
Imagínese
ahora, por ejemplo, que en el bastón anterior las dos bolas tienen
un muelle entre ellas. Aunque las bolas están separadas, se puede
hablar de su CG común, en la línea que conecta sus centros,
a 1/3 de la distancia del centro de la bola mayor.
(El CG del sistema Tierra-Luna se puede definir de la misma forma. Dado que la relación de masas de los dos cuerpos es de 81:1, el Cg es el punto sobre la línea entre sus centros dividiendo esta por su relación. Se puede mostrar que, despreciando la atracción del Sol y de los otros planetas, la Luna no orbita sobre el centro de la Tierra, sino, en cambio, sobre el CG común y lo mismo hace la Tierra, reaccionando a la atracción de la Luna. Por supuesto que, como la Tierra es mucho más pesada, el CG no está muy lejos del centro de la Tierra, de hecho está mas cercano que la propia superficie de la Tierra.)Suponga ahora que se coloca un fósforo encendido bajo el muelle, calentándolo. Cuando el muelle se expande, empuja hacia fuera las bolas, pero si es muy blando, su propio movimiento no importa y podemos asumir que las bolas se empujan mutuamente. Mediante la formulación de Mach de las ecuaciones del movimiento, si la bola más pesada recibe una aceleración a, la ligera recibe 2a, el doble. Para cada incremento en la velocidad de la bola pesada, la ligera recibe el doble, y se tiene que para cada momento, su velocidad total, al igual que la distancia cubierta, es la doble de la de la bola mayor. La conservación del momento conduce al mismo resultado. Si la bola pesada está a la distancia D de la posición inicial del muelle, la más ligera está a una distancia 2D, como en la figura anterior, reproducida aquí. No importa el tiempo que pase, el centro de gravedad continuará en el mismo punto. CohetesEsto se convierte en un principio general: en cualquier objeto ó serie de objetos, las fuerzas que solo involucran a esos objetos y a nada más ("fuerzas internas") no pueden mover al centro de gravedad.Un astronauta flotando en el traje espacial no puede cambiar su posición sin involucrar a algo más, p.e. apoyandose contra su nave. El centro de gravedad ó "centro de masa", es un punto fijo que no puede ser movido sin ayuda exterior (girar a su alrededor sí es posible). Arrojando una herramienta pesada en una dirección, el astronauta
podría moverse en la dirección opuesta, aunque el centro
de gravedad común de los dos permanecerá siendo el mismo.
Dándole una botella de oxígeno comprimido, se consigue el
mismo resultado al expulsar un chorro de gas (una escena que aparecía
en los antiguos filmes de ciencia ficción). Un cohete hace lo mismo,
excepto que se sustituye el gas frío por un chorro de gas reluciente,
mucho más rápido, producido por la combustión del
combustible apropiado.
Los poderosos cohetes que elevan cientos ó aún miles de toneladas desde la rampa de lanzamiento, dependen del mismo principio. Si alguna vez observó despegar un cohete desde Cabo Cañaveral, es importante recordar que si pudiera extraer de la escena la rampa de lanzamiento, la atmósfera y la Tierra, el centro de gravedad combinado del cohete y sus gases de escape permanecerán siempre donde comenzaron, en el punto de lanzamiento. Puede parecer una manera de producir movimiento en la dirección contraria. Pero todavía, los cohetes son (por lo menos por ahora) la única forma práctica de abandonar la Tierra y volar al espacio. --------------------------
Movimiento del CoheteSupongamos que tenemos un cohete de una masa total de 2M, de la cual M es la carga útil y M es el combustible. Al quemarse el combustible, este es expulsado con una velocidad promedio V relativa a lo que el cohete tenía al inicio.
Para evitar esto, (el obtener esto requiere cálculo) tan solo definamos la velocidad media V mediante la conservación del momento, sin intentar resolver su relación con la velocidad del chorro de escape v. Al agotarse el combustible, digamos que, el chorro ha impartido momento MV a la carga, y ha producido un momento igual y en dirección contraria.] La carga ahora ha ganado velocidad V. ¡Pero necesitamos más! De manera que construímos un cohete de masa 4M, de la cual 2M es combustible, mientras que la carga. también de masa 2M, es el pequeño cohete descrito arriba, el cual funciona para una segunda etapa. Cuando el combustible del cohete grande se termina, alcanzamos una velocidad V, entonces la segunda etapa se enciende, agregando otra V a la velocidad, para un total de 2V. ¡Aún más rápido! Ahora el cohete tiene una masa 8M de la cual 4M es combustible de la primera etapa, mientras que 4M es el cohete de dos estapas del diseño anterior. La primera etapa da una velocidad V, a lo cual las otras dos agregan 2V, para un total de 3V. Ahora ya puedes ver la tendencia. Si la masa de la carga final es M, entonces
Cada vez que la velocidad se incrementa una escala, la masa se duplica. No se pueden evitar este tipo de cosas al renunciar al uso de las etapas, digamos que el cohete de masa 8M, disparando todo el combustible de masa 7M en una sola detomación. Esto es debido a que (como ya se mostró), al ganar velocidad la carga (+ el combustible restante), se transfiere cada vez menos momento, el gas de escape primero tiene que sobreponerse al movimiento hacia adelante. De hecho, el resultado correcto (el cual utiliza cálculo) da el equivalente a un número grandísimo de pequeñas etapas, disparadas una después de la otra. Se obtiene de todas maneras el mismo resultado exponencial. Este es uno de los grandes problemas de los vuelos espaciales, especialmente con las primeras etapas, las cuales se elevan desde el suelo: aún una pequeña carga requiere un inmenso cohete. Tal vez algún día los exploradores espaciales podrán reducir algún peso del combustible mediante el uso de cohetes que utilicen aire ("scramjets"), pero esos parecen ser prácticos en el primer 1/4 a 1/3 de la velocidad orbital. Despegando desde un aeroplano de gran altura, como la nave de Burt Rutan, el "SpaceshipOne", o el "Pegasus", que es un cohete de combustible sólido, utilizado para el despegue de pequeños satélites, también ayuda a cortar la resistencia del aire, el cual es otro factor. Pero no hay otros atajos a la vista. Una vez en órbita, por supuesto, se pueden enlistar maneras más eficientes pero más graduales para generar fuerza de empuje, como la propulsión de iones.
-----------------------------------------------------
|