El problema básico de la trigonometría es algo parecido a esto: Está cerca de un ancho río y necesita conocer la distancia hasta la otra orilla, digamos hasta el árbol marcado en el dibujo por la letra C (para simplificar, ignoremos la 3ª dimensión). ¿Cómo hacerlo sin cruzar el río? La forma habitual es como sigue. Clave dos postes en el suelo en los puntos A y B y mida con una cinta la distancia c entre ellos (la "base"). |
|
Luego extraiga el poste del punto A y sustitúyalo por un telescopio
de topógrafo como el que se muestra aquí ("teodolito"), contando
con una placa dividida en 360 grados, marque la dirección ("azimut")
a la que apunta el telescopio. Dirigiendo el telescopio primero hacia el
árbol y luego hacia el poste B, mide el ángulo A del triángulo
ABC, igual a la diferencia entre los números que ha leído
de la placa de azimut. Sustituya el poste, lleve el teodolito al punto
B y mida de la misma forma el ángulo B .
La longitud c de la base y los dos ángulos A y B son todo lo que necesita para conocer el triángulo ABC, suficiente, por ejemplo, para construir un triángulo de la misma forma y mismo tamaño, en un sitio más conveniente. La trigonometría (de trigon = triángulo) en un principio fue el arte de calcular la información perdida mediante simple cálculo. Dada la suficiente información para definir un triángulo, la trigonometría le permite calcular el resto de las dimensiones y de ángulos. |
| ¿Por qué triángulos? Porque son los bloques
básicos de construcción para cualquier figura rectilínea
que se pueda construir. El cuadrado, el pentágono u otro polígono
puede dividirse en triángulos por medio de líneas rectas
radiando desde un ángulo hacia los otros.
Para topografiar una tierra los topógrafos la dividen en triángulos y marcan cada ángulo con un "punto de referencia", que hoy en día es, a menudo, una placa de latón redonda fijada en el suelo con un agujero en el centro, sobre el que ponen sus varillas y teodolitos (George Washington hizo este trabajo cuando era un adolescente). Después de medir la base, como la AB en el ejemplo del río, el topógrafo medirá (de la forma descrita aquí) los ángulos que se forman con el punto C y usar la trigonometría para calcular las distancias AC y BC. Estas pueden servir como base de 2 nuevos triángulos, que a su vez suministrarán bases para dos más..., y de esta forma construirá más y más triángulos hasta que se cubra la tierra al completo con una red que tiene distancias conocidas. Posteriormente se puede añadir una red secundaria, subdividiendo los triángulos grandes y marcando sus puntos con estacas de hierro, que proporcionarán distancias conocidas adicionales en las que se pueden basar los mapas o los planos. Un gran proyecto de reconocimiento de los 1800s fue la "Gran Planimetría Trigonométrica" de la India británica. Se construyeron para el proyecto los mayores teodolitos, monstruos con escalas circulares de 36" de ancho, cuyas lecturas se hacían con extraordinaria precisión con 5 microscopios. Cada uno con su caja pesaba media tonelada y se necesitaban 12 hombres para trasladarlo. Usándolos el proyecto cubrió el país con múltiples cadenas de triángulos en las direcciones norte-sur y este-oeste (las áreas entre las cadenas de dejaron para más tarde) y se necesitaron décadas para completarla. En 1843 Andrew Scott Waugh se encargó del proyecto como Inspector
General y puso especial atención a las montañas del
Himalaya del norte de la India. Debido a las nubes y a la niebla, esas
montañas se ven raramente desde las tierras bajas, y hasta 1847
no se consiguieron varias mediciones. Después de haberse hecho,
los resultados necesitaron ser analizados laboriosamente por "computadores"
en las oficinas de inspección; no eran máquinas sino personas
que efectuaban los cálculos trigonométricos.
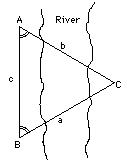
La historia dice que en 1852 el jefe de los "computadores" fue hacia
el director y le dijo: "Señor, hemos descubierto la mayor montaña
del mundo". Desde una distancia de más de 100 millas (160 km), se
observó la montaña desde seis estaciones diferentes, y "no
dio lugar a que el observador sospechara que estaba viendo a través
de su telescopio el punto más alto de la Tierra". Al principio se
la designó como "Pico XV" por la inspección, pero en 1856
Waugh la denominó en memoria de Sir George Everest, su predecesor
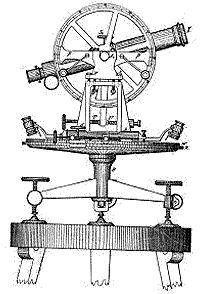
en la oficina de jefe de inspectores. El Everest fue el primero en registrarse
y en usar los teodolitos gigantes; ahora están expuestos en el "Museum
of the Survey of India" en Dehra Dum.
Hoy en día la posición sobre la Tierra se puede localizar
de forma muy precisa usando el sistema
de posicionamiento global (GPS) de 24 satélites en órbita
exacta, que están difundiendo constantemente su posición.
Un pequeño instrumento electrónico de mano recibe sus señales
y nos devuelve nuestra posición con un error de 10-20 metros ( aún
es más preciso para usos militares, los patrocinadores del sistema).
Se usa una gran cantidad de trigonometría, pero lo hace todo la
computadora que está dentro de su aparato, lo único que usted
necesita es pulsar los botones apropiados.
Ahora que conoce un poco de los usos de la trigonometría, bienvenido
a avanzar por lo esencial de ella.
Nota: Los detalles sobre el descubrimiento del Monte Everest
y la cartografía de la India están tomados de "Who
Discovered Mount Everest?" de Parke A. Dickey,
Eos (Transactions
of the American Geophysical Union), vol 66, p. 697-700, 8 Octubre 1985.
El artículo se volvió a imprimir en la p. 54-59 de la History
of Geophysics, Vol. 4, editada por C. Stewart Gillmor, publicada por
la American Geophysical Union, 1990. |
Se puede encontrar aquí un artículo erudito sobre la cartografía de la India (más allá de la historia narrada aquí, aunque existe alguna relación).
Sobre la denominación del Mt. Everest.
Una guía
del profesor para usar en clase la cartografía de la India y
el descubrimiento del Mt. Everest como una introducción a la cartografía.
La atribución de la denominación, sin embargo, es incorrecta;
vea el ítem precedente.
Página principal en Español (índice)Índice Matemático Linea del Tiempo Glosario . Próxima Etapa: #M-8 Como enunciar los Senos de los Cosenos
Author and Curator: Dr. David P. Stern
Last updated 13 December 2001
|
