Los triángulos tienen muchas formas. Puede ser difícil
clasificar los triángulos de formas arbitrarias, pero se debe observar
que cualquier triángulo ABC se puede dividir siempre en dos triángulos
con un ángulo recto, los triángulos con un ángulo
igual a 90°. Estos son más fáciles de tratar.
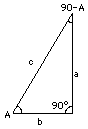
Los tres ángulos de un triángulo suman 180º (no lo vamos a probar aquí) y por consiguiente, en un triángulo con un ángulo recto y con ángulos agudos A y B A + B + 90° = 180° Restando 90° de ambos lados A + B = 90° Dado el valor de un ángulo A, el otro ángulo B se determina totalmente (es igual a 90°-A), y esta es la forma del triángulo, aunque no su tamaño. Denomine los lados de un triángulo (a,b,c), cada uno corresponde con el nombre de un ángulo enfrentado a él. El ángulo A no determina la longitud de ningún lado, sino que únicamente fija la proporción entre los lados. Esa proporción tiene nombre y existe una notación específica para escribirla: a/c = sen A -- "el seno de A"
Para diferenciarlos recuerde: El sen A tiene el lado opuesto al ángulo A como
numerador de su fracción
Existe una relación simple entre el seno y el coseno de cualquier ángulo. Por el Teorema de Pitágoras a2 + b2 = c2 Por consiguiente, para cualquier ángulo A (sen A)2 + (cos A)2 = (b2/c2) + (a2/c2) = (a2 + b2)/c2 = 1 Esta declaración se escribe normalmente como sen2A (no senA2, que se podría entender como el seno de un ángulo igual a A2): sin2A + cos2A = 1 Tanto senA como cosA deberán ser números menores que 1, los lados adyacente y opuesto de un triángulo son siempre menores que el lado opuesto al ángulo de 90° (llamado la hipotenusa, una palabra apreciada por los amantes de las bromas y los retruécanos). Cuando un ángulo A se acerca más y más a los 90° (y B se hace menor y menor), el triángulo se hace cada vez más estrecho y delgado. La longitud del lado a se acerca a c, mientras que la longitud de b se hace muy pequeña: sin embargo cuando A se acerca a los 90°, senA se aproxima a 1 y cosA a cero. Para el cálculo de otros valores, vea la sección siguiente. |