La tercera ley de Kepler nos permite evaluar las dimensions del sistema solar en unidades relativas, llamadas "unidades astronómicas" (UAs), en donde 1 UA es la distancia media entre el Sol y la Tierra. Sin embargo, para expresar la UA en kilómetros o en millas parece requerir algún tipo de paralaje--alguna diferencia entre la posición observada de algún objeto en el sistema solar, al ser visto desde dos puntos separados entre sí, cuya distancia entre ellos (en kilómetros o millas) es conocida. El problema es que los objetos planetarios están a unas distancias tan enormes, que el desplazamiento de su posición aparente, al ser vista desde dos puntos separados en la Tierra, es muy pequeña. Edmond Halley propuso utilizar el tránsito de Venus a lo largo del disco solar, al mostrarse como un mancha oscura redonda --o, para citar a un observador del tránsito de 2004, "como un arándano enfrente de una naranja". Este es un evento relativamente raro. Los tránsitos ocurren en pares con más de un siglo de separación: ninguno ocurrió en los 1900s, aunque uno ocurrió el 8 de Junio de 2004, con otro en 2012.
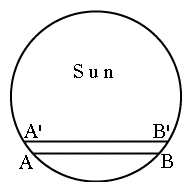
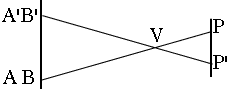
Suponga que un observador en el punto P en la Tierra ve a Venus cruzar el disco del Sol desde A hasta B (Figura 2 arriba--dos figuras, de frente y de lado). El movimiento de Venus a lo largo del disco del Sol es debido a los movimientos orbitales combinados de los dos planetas; de acuerdo a las leyes de Kepler, entre más cercano esté un planeta del Sol, se mueve más rápido, de manera que Venus se mueve más rápido que la Tierra, y esencialmente, durante un tránsito, éste le gana. La órbita de Venus está muy cercana al plano orbital de la Tierra, normalmente conocido como el plano de la eclíptica (parecido, pero no idéntico, de lo contrario ocurriría un tránsito cada vez que Venus se sobrepase en su giro a la Tierra). Por lo tanto la línea AB es casi paralela a la línea que denota la eclíptica en la esfera celestial, la linea a lo largo de la cual el plano de la eclíptica intersecta nuestra vista del cielo. Vista desde un punto diferente P', Venus se mueve a lo largo de A'B', esencialmente paralelo a AB. Ese punto diferente está preferiblemente en el lado opuesto del ecuador, lo cual hace más factible que lo coloque en el lado opuesto de la eclíptica también. Si medimos entonces la distancia D entre AB y A'B', en principio podemos aplicar alguna trigonometría simple para el paralaje y obtener la distancia PV entre P y la posición V de Venus. ¡Si tan solo la astronomía fuera tan fácil! En realidad, las líneas AB y A'B' están aún muy crecanas entre sí. La figura en la parte superior de la página (su fuente es aquí) contiene imágenes de Venus frente al Sol, obtenidas el 8 de Junio de 2004, desde 3 lugares, y cada juego de datos marcados con diferente color. Es evidente que las rutas están muy cercanas, menos de un radio de Venus de separación. Midiendo cada una por separado y obteniendo de ellas su separación D no es factible que nos de un resultado muy exacto. Lo que Halley notó fue que se podía obtener una información midiendo el paso de Venus desde A hasta B y desde A' hasta B'. Dado que la orilla ("limbo") del Sol se curva, la longitud AB es diferente de la de A'B' (decimos "longitud" por conveniencia--en realidad AB, A'B' y D son todas ángulos visuales). La velocidad aparente del movimiento de Venus a través del Sol es casi la misma que cuando se ve desde cualquier lugar de la Tierra, de manera que obteniendo la diferencia en tiempo entre los cruces de AB y A'B', la distancia se puede deducir también. Esto es más sensible porque la duración del tránsito es horas, mientras que la diferencia del tiempo del tránsito puede ser de tan solo minutos. Tales duraciones pueden ser (en principio) medidas con bastante exactitud. En estas secciones destacaremos un procedimiento simplificado para obtener la unidad astronómica a partir de los tiempos de tránsito del 8 de Junio de 2004, utilizando duraciones predecidas de los tránsitos. Los astrónomos que calcularon dichas duraciones, disponibles en la web aquí--utilizaron por supuesto el bien establecido valor de la unidad astronómica, haciendo esta tan solo un ejercicio. Si esto hubiera sido un cálculo "real", los valores observados habrían sido utilizados. Este será un cálculo a grandes rasgos, utilizando presupuestos simplificados y despreciando correcciones que en las determinaciones completas se pueden necesitar. Dado que somos libres de selecionar los puestos de observación, escogimos dos a casi la misma latitud y longitud al norte y sur del ecuador. Ambos están en África (latitud y longitud con medio grado de diferencia).
Esta simetría de posiciones simplifica el análisis. Como se observó arriba, el movimiento de Venus a lo largo de la cara del Sol es casi por completo debido a los movimientos orbitales de la Tierra y Venus. Teniendo la Tierra una velocidad orbital de 30 km/s, uno puede pensar que la velocidad que brinda la Rotación de la Tierra se puede despreciar, dado que típicamente se cuantifica en unos pocos de cientos de metros/seg. Sin embargo, esa velocidad mueve al observaodr durante la duración completa del tránsito, totalizando más de 5 horas. Durante ese tiempo algunos observadores se pueden desplazar tanto como un radio de la Tierra, y la diferencia en desplazamiento entre los observadores en las diferentes latitudes puede alcanzar varios miles de kilómetros. Por otro lado, la información de la cual se obtiene la unidad astronómica está contenida en una diferencia de tiempo ΔT de tan solo 5 minutos, durante la cual la Tierra se mueve aproximadamente Un desplazamiento adicional de unos pocos de miles de km. podría degradar seriamente el resultado, y puede requerir una corrección adicional. Para simplificar aquí el cálculo, simplificamos el problema seleccionando dos sitios a igual distancia del ecuador, y por lo tanto con iguales velocidades de rotación. Escogiendo casi la misma longitud también estandariza las velocidades con respecto a Venus y el Sol. Así ambos tiempos de tránsito son afectados de manera igual, y ΔT será utilizada sin correción adicional. Este sitio weba está ligado a otros dos. La siguiente página ofrece la solución de D. El cálculo requiere algo de la trigonometría desarrollada en la " Revisión Matemática" y en particular las fórmulas para el seno y el coseno de la suma de ángulos, obtenidos en la sección M-11. La página que sigue ofrece un valor aproximado de la unidad astronómica. Debido a las aproximaciones utilizadas, el resultado se desvía varias unidades de porcentaje, pero no requiere herramientas matemáticas más allá de aquellas cubiertas aquí. También encontrará algunas de las complicaciones con las que los astrónomos se enfrentan. Archivo de fotos del tránsito (incluyendo una foto que captó un avión en vuelo). Haga click aquí para ver para ver una gran colección de vínculos relacionados con el tránsito de Venus.
|
![[IMAGEN: Imagen del Tránsito de Venus]](Sfigs/Venus2.gif)