|
Esta página es una cotinuación de El Tránsito de Venus--Introducción, y utiliza la misma notación.
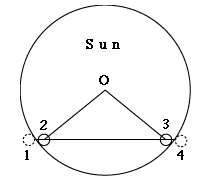
Las predicciones para el tránsito dan cuatro tiempos de "contacto", en los cuales el disco oscuro de Venus, toca la orilla del disco del Sol, (marcados mediante números en la Figura 3).
Obviamente, Venus no es visible durante el primer y cuarto contacto, de manera que usamos el segundo contacto para definir A o A' y el tercer contacto para definirB o B' (vea figura). El disco del Sol tiene un diámetro aparente 2R de aproximadamente 31.5 minutos de arco, y el radio r de Venus es de aproximadamente 1 minuto. De acuerdo a lo que se vió para AB, etc., en una página anterior, R y r no son distancias, sino ángulos visuales. Aún así, en este cálculo todos los ángulos pueden ser manejados como distancias, debido a que son muy pequeños. Se puede imaginar la figura 3 proyectada hacia la parte interior de una esfera inmensa (por ejemplo el domo de un planetario, o en la misma esfera celestial). Un área de medio grado, el cual es el diámetro aproximado del Sol, cubre una parte tan pequeña de la totalidad de la esfera, que haciendo una buena aproximación, esta se puede ver como si fuera plana, y las distancias en ella son muy proporcionales a los ángulos que cubren. Escogimos que los puntos A y B no estuvieran en la orilla ("limbo") del disco del Sol durante el segundo y tercer contacto, sino en el centro de Venus en esos momentos. Si O es el centro del Sol, esos puntos descansan en un círculo alrededor de O con un radio de (R–r). Así, el tiempo para cubrir AB determina el paso de Venus a lo largo de una cuerda (= corte recto a través de un círculo) de un "Sol reducido" que cubre tan solo 30.5 minutos de arco.
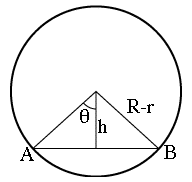
También necesitaremos un valor moderadamente exacto de la distancia h de la línea AB desde el centro O, o, más convenientemente, el ángulo θ (Griego teta; vea la Fig. 4 abajo), la mitad del ángulo cubierto por AB. Obteniéndola de las fotografías publicadas (en este caso, la versión publicada de la Fig. 1 de la página anterior, o simulaciones como la que fue provista por la Univ. de Lancashire) produce aproximadamente 46.4 grados. Entonces (Figura 4 abajo)
Dado que el tiempo T del tránsito es proporcional a la distancia (AB), podemos escribir
donde k es algún factor de proporcionalidad. Su valor no será necesario, dado que nos enfocamos a utilizar la proporción entre T y la diferencia ΔT en los tiempos de tránsito en las dos ubicaciones, y al obtener la proporción, k se cancela. Utilizando trigonometría
Si la línea A'B' de la estación exterior es ligeramente más larga, esta cubre un ángulo 2(θ+δ) ligeramente más largo, y su distancia desde O no es h sino = (R–r)(cosθ cosδ – senθ senδ ) (3) Si δ es un ángulo muy pequeño, senδ también es pequeño. Pero aún y cuando un valor pequeño de senδ continúe siendo suficientemente importante para ser incluído, cosδ es probablemente tan cercano a 1 que se puede remplazar con seguridad con 1. Para demostrar esto, note que Recordandoque la raíz cuadrada es también la potencia a la (1/2), de acuerdo al teorema binomial Asi que, si aproximamos cosδ a 1, el error realizado es tan solo del orden de sen2δ lo cual (es verdadero para número pequeños) es mucho más pequeño que senδ. Si al expresar h', mantenemos senδ pero reemplazamos cosδ con 1, entonces para tener una buena aproximación de donde El tiempo de tránsito en el punto P' es obtenido de una manera similar a la ecuación (2) = 2k (R–r)(senθ cosδ + cosθ senδ ) y para la misma buena aproximación que la anterior, con el ángulo δ pequeño
Así = cosθ senδ / sen θ (6) Esto era justo lo que esperábamos: la pequeñez de la proporción a la izquierda se balancea con lo pequeño de senδ a la derecha. Extrayendo ese término Esto puede ser sustituído en la ecuación (4) para D, otro valor pequeño Eso es lo que necesitábamos. Tal y como Halley propuso, la separación D entre las rutas del tránsito está ahora expresada en términos de la diferencia observada entre los tiempos de tránsito, así como de la longitud de tiempo T del tránsito observado (o su promedio (T + T')/2) así como el ángulo θ, dando la distancia de la ruta del tránsito desde el centro del Sol. |