Site Map
Lesson plan
Glossary
Timeline
Questions & Answers
Central Home Page


(17b) Comparing Masses Without Use of Gravity

    Index

16. Newton's Laws

17. Mass

17a. Measuring Mass
        in Orbit
       
17b. Inertial balance

18. Newton's 2nd Law

18a. The Third Law

18b. Momentum

18c. Work

18d. Work against
        Electric Forces 		With only the simplest equipment, you too can perform mass measurements similar to the ones aboard Skylab.

You will need:

  • A hacksaw blade

  • A small workshop vise, or an equivalent tool; the jaws should move horizontally.

  • A medium-size (1.25 inch wide) binder clip, as is used in offices to hold papers together--the type made of flat blue steel, with two wire handles.

  • Compact heavy objects whose mass is to be measured. I used two large bolts, weighing 50 and 120 grams.

  • A watch capable of counting seconds.

  • Small scales (I used kitchen scales measuring 0-500 gram)

    • The mass comparison experiment     (clamped to the leg of a table)

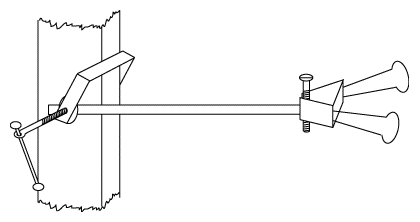    Instructions

    1. Securely clamp one end of the blade in the vise, so that the rest of it sticks out horizontally (sawteeth downwards, for safety). The blade should be able to bend sideways, but not up and down.

    2. Clamp the binder-clip to the free end of the sawblade and use it to attach one of the weights.

    3. Pull the weight a short distance to one side and let go. Count the number of oscillations in 10 or 20 seconds.

    4. Repeat with the other weight.

    5. Using the scales, find the weights m1 and m2 of the two weighed objects, and also the weight m0 of the binder clip used to attach them.

    The theory predicts that the oscillation period should be proportional to the square root of the oscillating mass, including the mass of the clip. Note that gravity plays no part here: the oscillation period would be the same on the Moon or in zero-g.

    Denoting square root by SQRT, we have

            (T2/T1) = SQRT(m2+m0)/SQRT(m1+m0) = SQRT[(m2+m0)/(m1+m0)].

    ("The ratio of square roots is the square root of the ratio"). Muliplying each side by itself:

            (T2/T1)2 = (m2+m0)/(m1+m0).

    If we were in space, measured T1 and T2, and knew the masses m1 and m0, then we could calculate an unknown mass m2.

    Result of an actual measurement:

    Weights: m1 = 50 gr, m2 = 120 gr, m0 = 10 gr.

    The number of oscillations counted in a 10-second period was: with m1, 20 oscillations, with m2, 13.5 oscillations. Then

       T1 = 10 sec/20 = 0.5 sec           T2 = 10 sec/13.5 = 0.74074 sec.

    so that

        (T2/T1)2 = 2.195   should equal   (m2+m0)/(m1+m0) = 130/60 = 2.167

    This agreement is probably better than such a crude experiment deserves, considering that the mass of the sawblade itself was ignored.

    Next Stop: #18 Newton's Second Law

                Timeline                     Glossary                     Back to the Master List

    Author and Curator:   Dr. David P. Stern
         Mail to Dr.Stern:   stargaze("at" symbol)phy6.org .

    Last updated: 9-21-2004
    Reformatted 24 March 2006