(19) Il moto circolare

    In assenza di forze, un moto rettilineo uniforme continua indefinitamente. Un moto circolare, invece, richiede una forza per proseguire.

    Immaginiamo di aver legato un sasso a una corda, e di farlo roteare in modo che descriva un cerchio di un certo raggio R (in metri). Ogni giro il sasso percorrerà una distanza

2 πR metri

dove π = 3,14159265359. . . è il rapporto tra la circonferenza e il diametro di un cerchio (per ricordare facilmente a memoria le prime cifre di π, basta contare le lettere nella frase: "Già, è bene e utile ricordare le dodici cifre del greco parametro").

    Immaginiamo inoltre che il sasso compia N giri ("rivoluzioni") al secondo. Poiché la sua velocità v è pari alla distanza percorsa in un secondo, si trova

v = 2 πNR m/sec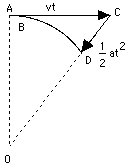

    Se si considera soltanto un brevissimo istante del suo moto, il cammino AB percorso è così corto che si può trascurare la sua curvatura, consentendoci di assimilare il moto a un tratto rettilineo, percorso con velocità v. Dopo un poco, tuttavia, la differenza tra il moto reale e un tratto rettilineo diventa evidente: il moto rettilineo con velocità v porterebbe l'oggetto ad un punto C, alla distanza

AC = vt

mentre il moto reale lo porta ad un punto D su una circonferenza, il cui centro indicheremo con O.

    È utile considerare questo moto come la somma di due diversi moti: un moto rettilineo da A a C, e un altro moto che si aggiunge a questo da C a D, che riporta l'oggetto sulla circonferenza. Come si è notato in precedenza (ved. la sezione sui vettori), quando un moto è la combinazione di due moti semplici, lo spostamento risultante può essere ottenuto ricavando separatamente gli spostamenti dovuti da ciascuno dei due moti considerato a sé stante, e poi addizionandoli tra loro.

    Il moto da C a D che viene aggiunto è quello che qui ci interessa. La sua direzione è sempre verso il centro, e la distanza CD percorsa -- indicata qui con x -- può essere ottenuta dal teorema di Pitagora applicato al triangolo OAC (il calcolo è simile a quello che fornisce la distanza dell'orizzonte nella sezione (8a)). In tale triangolo, OA = R, AC = vt, OC = R + x. E quindi

R² + v²t² = (R + x)² = R²+ 2Rx + x²

Sottraendo R² da entrambi i membri

v²t² = 2Rx + x² = x(2R + x)

Se l'intervallo di tempo t è molto breve, x è molto più piccolo di 2R e può quindi essere trascurato nella somma. Pertanto

v²t² = 2xR

oppure

x = 1/2 (v²/R) t²

Da una precedente formula, nella sezione riguardante l'accelerazione, questa è esattamente la distanza percorsa nel tempo t in un moto con accelerazione

a = v²/R

    Questo risultato suggerisce che un moto circolare uniforme, almeno per un breve periodo di tempo, può essere considerato come la somma di un moto rettilineo con velocità costante v, più un moto accelerato diretto verso il centro di rotazione, con un'accelerazione a, data dalla precedente formula.

    La conclusione è corretta, anche se il procedimento per ricavarla è piuttosto irregolare. Il procedimento convenzionale per arrivare a questa conclusione (come pure per la maggior parte dei moti) richiede l'uso del calcolo differenziale, lo studio cioè delle quantità che variano e del modo con cui variano, oltre a una buona familiarità con i vettori.