(8c) Quanto è lontana la Luna?--1

  Aristarco intorno al 270 a.C. ricavò la distanza della Luna dalla durata di una eclisse lunare (Ipparco più tardi ricavò tale distanza con un altro metodo).

    A quei tempi era comunemente accettato che la Terra fosse una sfera (benché le sue dimensioni furono calcolate solo alcuni anni più tardi da Eratostene). Gli astronomi credevano anche che la Terra si trovasse al centro dell'universo, e che il Sole, la Luna, i pianeti e le stelle le girassero intorno. Era quindi naturale che Aristarco assumesse che la Luna percorresse un'ampia orbita circolare attorno alla Terra.

    Sia R il raggio di quell'orbita e T il tempo impiegato dalla Luna a compiere un giro completo, pari a circa un mese. In questo tempo, la Luna percorre una distanza di 2πR, dove π ~ 3,1415926... è una costante matematica, pari al rapporto tra una circonferenza e il suo diametro.

    Un'eclisse di Luna si verifica quando la Luna passa nell'ombra della Terra, in posizione opposta al Sole (e quindi deve essere Luna piena). Se r è il raggio della Terra, il diametro dell'ombra sarà molto vicino a 2r. Indichiamo con t il tempo che occorre perché il punto centrale della Luna attraversi il centro dell'ombra, circa 3 ore (nelle eclissi di massima durata, quando la Luna attraversa il centro dell'ombra).

    Nell'ipotesi che la Luna si muova attorno alla Terra a velocità costante -- e quindi impiegherà un tempo T per coprire 2π R ~ 6,28R, e un tempo t per coprire 2r -- allora

Da questa relazione Aristarco ottenne

che è in accordo con la distanza media della Luna conosciuta oggi, di 60 raggi terrestri.

Qualche altro dettaglio

    Vista dalla Terra, la "Luna nuova" (che avviene tra il momento in cui una piccola falce è ancora visibile prima del sorgere del Sole e il momento in cui si vede già una nuova piccola falce dopo il tramonto del Sole) si verifica quando la Luna, nel suo moto apparente attraverso il cielo, sorpassa il Sole. Tuttavia, fino al verificarsi della successiva Luna nuova, la posizione del Sole è intanto un po' cambiata. Se il Sole impiega 12 mesi a fare un giro completo nel cielo (lungo l'eclittica o, che è lo stesso, lungo lo zodiaco), allora in un mese compie 1/12 del suo giro. La Luna deve quindi compiere [1+(1/12)] di giro per raggiungere di nuovo il Sole, e il mese lunare ("periodo sinodico") è circa 1/12 di mese più lungo del periodo effettivo di 27,32 giorni.

    Inoltre, l'ombra della Terra ha un diametro che è solo approssimativamente pari a 2r. Sarebbe molto prossimo a 2r se il Sole fosse una sorgente luminosa puntiforme (lo sarebbe esattamente se il Sole si trovasse a distanza infinita). In realtà, invece, il Sole è abbastanza esteso da apparire come un disco che copre circa mezzo grado nel cielo. Come conseguenza, l'ombra della Terra non è un cilindro, ma un cono che si restringe e, alla distanza della Luna, è già di circa il 25% più stretta di 2r.

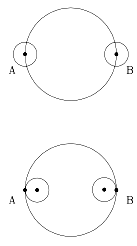
    Vi è un altro modo di considerare il fenomeno. Supponiamo di osservare l'eclisse dalla Luna. Vista da là, la Terra si muove da est verso ovest -- da A a B nel disegno, assumendo che l'eclisse sia della massima durata (cioè che il centro della Terra passi davanti al Sole).

    L'eclisse comincia quando l'ultimo lembo del bordo occidentale del Sole supera il punto A (ved. parte inferiore del disegno) e termina quando il primo lembo del bordo orientale del Sole si affaccia dal punto B. Questo richiede meno tempo di quello impiegato dal centro del Sole per passare da A a B (ved. parte superiore del disegno), che sarebbe la durata dell'eclisse se il Sole fosse una sorgente puntiforme, posizionata nel suo centro.