L'eclisse
|
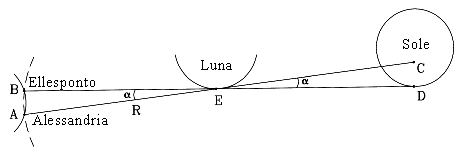
Ipparco, che usò un'eclisse lunare per ricavare la precessione degli equinozi (ved. qui), usò un'eclisse totale di Sole, probabilmente quella del 129 a.C., per valutare la distanza della Luna. Tale distanza fu anche ricavata da Aristarco (ved. qui). Quella eclisse era totale presso l'Ellesponto (lo stretto dei Dardanelli, quello stretto che separa la parte europea della Turchia dalla parte asiatica), ma soltanto i 4/5 del Sole erano coperti dalla Luna ad Alessandria d'Egitto, un po' più a sud. Ipparco sapeva che, durante una eclisse solare, il Sole e la Luna occupano lo stesso punto della sfera celeste. Il motivo - secondo il ragionamento di Ipparco - era che la Luna passa tra noi e il Sole. Egli era convinto che il Sole fosse molto più lontano della Luna, come aveva concluso Aristarco di Samo, circa un secolo prima, osservando il momento in cui la Luna era esattamente nella fase del primo o ultimo quarto (ved. le sezioni #8c and #9a). Egli suppose anche che il massimo dell'eclisse avvenisse nello stesso momento in entrambe le località (non è sempre così, ma fortunatamente non era molto lontano dal vero), e quindi eseguì il seguente calcolo. |

|
Durante una eclisse totale di Sole, la Luna copre appena il disco solare. Il Sole stesso è così lontano che, quando viene osservato da un punto qualsiasi della Terra, copre praticamente la stessa zona di cielo, con un'ampiezza di circa 0,5°. Ipparco considerò in particolare il punto E sul bordo della Luna (ved. disegno), che, durante la totalità, quando era osservato dall'Ellesponto (punto B), si sovrapponeva esattamente al punto D sul bordo del Sole. Visto da Alessandria (punto A), nello stesso momento, il punto E si sovrapponeva soltanto al punto C all'interno del disco solare, a circa 1/5 di diametro solare dal bordo -- ed era questo il motivo per cui l'eclisse laggiù non era totale. Un quinto di diametro solare copre circa 0,1° in cielo, per cui il piccolo angolo α (alfa) tra le due direzioni è di circa 0,1 gradi. Tale angolo è la parallasse del bordo della Luna, visto dalle due località. E' poco probabile che Ipparco conoscesse la distanza AB, ma presumibilmente conosceva la latitudine dell'Ellesponto e di Alessandria. Può essere dimostrato che la latitudine locale è uguale all'altezza del polo celeste sull'orizzonte, e ai nostri giorni può essere facilmente ricavata osservando l'altezza della Stella Polare sull'orizzonte. Al tempo di Ipparco il polo celeste non si trovava vicino alla Polare (a causa della precessione degli equinozi), ma Ipparco, che aveva disegnato una mappa con le posizioni di circa 850 stelle, doveva conoscere piuttosto bene la sua posizione. La latitudine dell'Ellesponto (da un moderno atlante) è di circa 40° 20' (40 gradi e 20 minuti, 60 minuti per grado), mentre quella di Alessandria d'Egitto è di circa 31° 20', con una differenza di 9°. Assumiamo anche che Alessandria sia esattamente a sud (cioè su uno stesso meridiano). Se inoltre r è il raggio della Terra, allora la circonferenza terrestre è 2πr, dove π = 3,1415926... ("pi greco") è il rapporto tra una circonferenza e il suo diametro. Poiché in una circonferenza vi sono 360°, si ottiene
dove il punto indica la moltiplicazione (l'equivalente algebrico del simbolo ×). La distanza R della LunaI punti A e B stanno anche su un'altra circonferenza centrata sulla Luna. Il raggio in questo caso è la distanza R tra la Terra e la Luna, e, poiché l'arco AB corrisponde a 0,1°, si ha
A voler essere precisi, ciascuno dei due archi di cerchio AB presenti nelle precedenti equazioni è misurato su una diversa circonferenza, con un diverso raggio (e le due circonferenze sono curvate in direzioni opposte). Tuttavia, in entrambi i casi AB corrisponde soltanto a una piccola parte della circonferenza, per cui possiamo approssimare ciascuno dei due archi al segmento AB. Con questa approssimazione possiamo considerare uguali le due espressioni e scrivere
Moltiplicando entrambi i membri per 360 e dividendo per 2π si ottiene
e questo suggerisce che la distanza della Luna sia pari a 90 raggi terrestri, sovrastimando il valore di circa il 50%. Un calcolo più accurato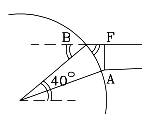 Un motivo per cui si è ottenuto un valore eccessivo sta nel fatto che si è assunto che la Luna si trovasse a perpendicolo in A e B. In realtà è probabile che la Luna si trovasse a un certo angolo rispetto alla verticale, cioè rispetto allo "zenit" (ved. disegno).
Un motivo per cui si è ottenuto un valore eccessivo sta nel fatto che si è assunto che la Luna si trovasse a perpendicolo in A e B. In realtà è probabile che la Luna si trovasse a un certo angolo rispetto alla verticale, cioè rispetto allo "zenit" (ved. disegno). Pertanto la sezione intercettata dall'angolo α sul cerchio di raggio R centrato in E non è AB ma AF (secondo disegno), che è più piccola. Tenendo conto di questo, la distanza si riduce. Non sappiamo dove si trovava il Sole durante l'eclisse del 129 a.C., ma comunque doveva trovarsi sull'eclittica (come dice il nome!), e quindi entro 23,5° dall'equatore celeste, da una parte o dall'altra. Assumendo che fosse sull'equatore (cioè che si trovasse a perpendicolo sull'equatore terrestre) e, secondo la cronaca delle osservazioni, in direzione sud (cioè l'eclisse avvenne verso mezzogiorno), si può fare una stima grossolana della correzione da apportare, usando della semplice trigonometria (ved. la sezione M-8). L'Ellesponto è situato a una latitudine di circa 40 gradi, e, come mostra il disegno, questo valore è anche quello dell'angolo tra la direzione della Luna e lo zenit. Dal disegno (il punto indica la moltiplicazione)
Ripetendo il calcolo precedente per AF
e alla fine Nota (15 Ott. 2004)Secondo il francese Mr. Léo Dubal, l'eclisse osservata da Ipparco avvenne il 20 novembre dell'anno 128 a.C. alle 15:30. I suoi dati potrebbero consentire valutazioni più accurate (anche se Ipparco probabilmente non possedeva i mezzi per migliorare ulteriormente le sue stime).Mr. Dubal ha un sito http://www.archaeometry.org con un collegamento a un elenco in cui ha ricostruito località, durate, date e orari di antiche eclissi. Per una discussione approfondita riguardo l'uso di questa e di altre antiche eclissi per ricavare l'andamento della rotazione terrestre, si può consultare una sua pagina Web qui. Commenti finaliSecondo "Una storia dell'astronomia" di A. Pannekoek, il risultato ottenuto da Ipparco era tra 62 e 73 raggi terrestri. Oggi sappiamo che la distanza media tra la Terra e la Luna è di circa 60 raggi terrestri, con una variazione di qualche raggio terrestre, a causa dell'ellitticità dell'orbita lunare.In mancanza di un cronometraggio accurato, è quasi garantito che il metodo produca una sovrastima della distanza. La Terra ruota sotto l'ombra proiettata dalla Luna, per cui quest'ombra si sposta su una larga striscia di territorio, coprendo differenti aree in differenti momenti. L'Ellesponto era soltanto una delle località in cui l'eclisse era totale. Similmente, Alessandria era soltanto una delle località in cui i 4/5 del disco solare erano oscurati. Scegliendo a caso un punto B tra le località del primo gruppo e un punto A tra le località del secondo gruppo, potrebbe ottenersi una linea di base molto più lunga e una distanza (errata) della Luna molto più grande. Il fatto che Alessandria si trovi quasi esattamente a sud dell'Ellesponto non garantisce che il massimo dell'eclisse avvenga nello stesso momento nelle due località, o che comunque i due istanti non siano molto lontani tra loro.
|
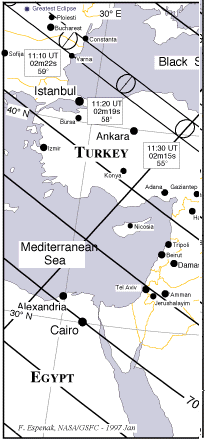
La storia si ripete?L'eclisse totale di Sole dell'11 agosto 1999 fu visibile solo a poche centinaia di chilometri a nord della zona usata da Ipparco. Il percorso della totalità si estendeva dall'Oceano Atlantico, vicino alle coste della Nuova Inghilterra, attraverso l'Inghilterra e l'Europa centrale, fino all'India. Qui a destra è riportata una mappa della zona interessata dall'eclisse -- la linea doppia indica il contorno della zona di totalità, e le varie linee parallele corrispondono alle località dove il Sole era eclissato del 90%, dell'80%, ecc. Come si vede, il percorso della totalità passava sul Mar Nero alle 11:15 del Tempo Universale (alle 13:15 del tempo locale) a circa 300 km a nord-est dell'Ellesponto, mentre ad Alessandria d'Egitto era eclissato soltanto il 71% del disco solare (anziché l'80% come nell'eclisse osservata da Ipparco) attorno alle 11:35.Con un po' di lavoro (un procedimento più veloce è riportato più avanti) è anche possibile ripetere i calcoli di Ipparco per l'eclisse del 1999 (conviene usare una calcolatrice, se è possibile).
|
|
Esiste anche un procedimento più rapido. Si nota dalla mappa che all'Ellesponto l'11 agosto 1999 il Sole era eclissato per il 90%, il che significa che in quella località, nel campo di vista di un osservatore, il bordo anteriore della Luna era distante dal bordo del disco del Sole di un 10% del diametro solare. Ad Alessandria lo stesso ragionamento mostra che il bordo della Luna era del 29% distante dal bordo del disco solare. Le linee di vista dalle due località al bordo della Luna, nel momento massimo dell'eclisse, formavano quindi un angolo pari al 19% del diametro visuale del Sole -- valore molto vicino al 20% ottenuto da Ipparco! Come si vede dalla mappa, il percorso della totalità l'11 agosto 1999 passava su Bucarest, la capitale della Romania. Il governo romeno volle commemorare l'evento riproducendo una mappa con la striscia di totalità sulla Romania (proseguendo quella disegnata più sopra in questa pagina) su una banconota da 2000 Lei. Si può fare clic qui per vedere un'immagine di quella banconota (occupa circa 70 Kb di memoria). Ulteriori dettagli su questa eclisse si possono trovare sul sito http://sunearth.gsfc.nasa.gov/eclipse/TSE1999TSE1999.html. Un sito Web relativo all'eclisse del 26 febbraio 1998, realizzato dalla rivista "Sky and Telescope", di tipo "fumetto", fornisce molti dettagli validi in generale per ogni eclisse solare. |
Il prossimo argomento: #9a E' la Terra che gira intorno al Sole?
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 21 Ottobre 2005