Oltre alla Luna, che è l'unico satellite naturale, la Terra ha ora molti satelliti artificiali, messi in orbita dagli uomini per svariati scopi. Il calcolo applicato da Newton alla Luna può essere usato anche per questi.
La velocità orbitale
Supponiamo che la Terra sia una sfera perfetta di raggio 1 Rt = 6 317 000 metri e non abbia atmosfera. In linea di principio, un satellite potrebbe allora orbitare appena al di sopra della sua superficie. La Terra lo attrarrebbe verso il basso con una forza F = mg, e, a causa della direzione di questa forza, anche ogni accelerazione sarebbe orientata nella direzione alto-basso.
Se un satellite è in un'orbita circolare stabile e la sua velocità è v, allora F fornisce l'esatta quantità di attrazione per mantenere il suo moto. E questo significa che
mg = F = mV2/Rt
Dividendo entrambi i membri per m, si vede che la massa del satellite non influisce, e resta
V2/Rt = g
Moltiplicando ora ambo i membri per Rt si ottiene:
V2 = (g) (Rt) = (9,81) (6 371 000) = 62 499 510 (m/sec2)
V = 7905,66 m/sec = 7,90566 km/s = Vo
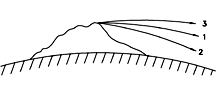
Questa è la velocità che occorre al satellite per rimanere nella sua orbita ("1" nel disegno). Se la velocità diminuisce, il satellite perde quota e urta contro la Terra ("2"), se invece aumenta, il satellite sale a una distanza maggiore ("3"). Per confronto, basti pensare che un aviogetto di linea vola a circa 250 m/sec, e un proiettile di fucile viaggia a circa 600 m/sec.
Abbiamo ora la necessità di introdurre di nuovo una radice quadrata. La radice quadrata di 2 corrisponde a circa
√(2) = 1,41421. . .
Se la velocità V del nostro satellite è soltanto moderatamente maggiore di Vo, allora la curva "3" del disegno sarà una porzione di una ellisse kepleriana e alla fine il satellite si riavvicinerà alla Terra. Se però V è maggiore di 1,4142... volte Vo, il satellite avrà raggiunto la velocità di fuga e non tornerà mai indietro: questo avviene a circa 11,2 km/sec.
Il valore di 11,2 km/s era stato già ricavato nella sezione sulla 2ª legge di Keplero, dove era stata introdotta (senza dimostrazione) l'espressione dell'energia del moto kepleriano pari a
E = 1/2 mv2 – k m/r
dove per un satellite in orbita attorno alla Terra a una distanza di un raggio terrestre Rt, la costante k è uguale a k=gRt2. L'energia è negativa per un veicolo spaziale catturato dalla gravità terrestre, positiva per uno non trattenuto affatto, e zero per uno che sia appena in grado di sfuggire. Sia V1 la velocità di un tale veicolo spaziale, posto a una distanza Rt ma con zero energia, cioè E=0. Allora
(1/2) m V12 = mgRt
da cui
V12 = 2gRt
che fornisce, come si era affermato
V1= 1,414×V0
La terza legge di Keplero per i satelliti terrestri
La velocità per un'orbita circolare attorno alla Terra per ogni distanza r si può calcolare in modo simile, ma occorre considerare che la la forza di gravità è più debole a distanze maggiori, di un fattore (Rt/r)2. Quindi abbiamo
V2/r = g (Rt r)2 = g Rt2/r2
Sia T il periodo orbitale, espresso in secondi. Allora (come notato precedentemente), la distanza 2πr percorsa in un'orbita è uguale a VT