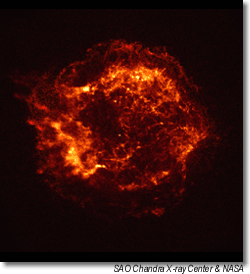
(10) Keplero e le sue leggiTycho Brahe (1546-1601)Tycho era un nobile danese interessato di astronomia. Nel 1572 apparve nel cielo una "nuova stella" (in linguaggio moderno una "nova"), non molto lontana dalla Polare, più luminosa di tutte le altre. Tycho misurò accuratamente la sua posizione, quindi la misurò di nuovo dopo 12 ore, quando la rotazione terrestre aveva spostato il punto di osservazione sull'altro lato della Terra. Era già noto che un tale spostamento faceva variare la posizione della Luna nel cielo, e aveva aiutato gli astronomi a valutare la sua distanza. Però la posizione della "nuova stella" non era variata, suggerendo quindi che si trattava di un oggetto molto più distante della Luna (si può fare clic qui per il resto della storia).
Il giovane Tycho fu così impressionato da questo evento che decise di dedicare la sua vita all'astronomia. Il Re di Danimarca lo incoraggiò e gli donò l'isola di Hven per costruirci un osservatorio, e le tasse riscosse sull'isola servirono a finanziare questa struttura. Il telescopio non era stato ancora inventato, e tutte le misure venivano compiute ad occhio, con l'aiuto di mire ottiche (simili ai mirini dei fucili) che potevano scorrere lungo dei cerchi graduati. Tycho portò tali metodi al massimo delle loro possibilità, cioè alla risoluzione dell'occhio umano, e le sue mappe stellari erano molto più accurate di qualunque altra mappa realizzata fino allora. Egli misurò, e ne tenne conto, perfino i piccolissimi spostamenti della posizione delle stelle vicino all'orizzonte, dovuti alla rifrazione della luce nell'atmosfera terrestre, simile a quella che avviene nel vetro o nell'acqua. Le sue osservazioni dei pianeti divennero la prova più schiacciante della teoria copernicana, contro quella tolemaica. Per quanto riguarda quelle teorie, Tycho credeva che tutti i pianeti ruotassero attorno al Sole, ma che il Sole ruotasse attorno alla Terra. Questa visione era in accordo con quella della Chiesa Protestante danese, poiché Martin Lutero, iniziatore della Riforma Protestante, aveva rifiutato la teoria di Copernico (che era suo contemporaneo). Tuttavia l'atteggiamento di Tycho era arrogante, e i residenti di Hven si lagnarono, così che dopo la morte del Re, che era stato il suo protettore, Tycho fu costretto a lasciare la Danimarca.
Nel 1599 si stabilì a Praga -- ora capitale della Repubblica Ceca, allora era la sede della corte dell'Imperatore tedesco Rodolfo -- e lì divenne astronomo di corte. E fu proprio a Praga dove un astronomo tedesco, di nome Giovanni Keplero, fu assunto da Tycho per svolgere i suoi calcoli. Quando nel 1601 Tycho morì improvvisamente, fu Keplero a continuare il suo lavoro. (Altre notizie e collegamenti riguardanti Tycho.)Giovanni Keplero (1571-1630)Keplero aveva studiato astronomia molto prima di incontrare Tycho: era a favore della teoria copernicana ed era in corrispondenza epistolare con Galileo. Le osservazioni di Tycho comprendevano anche alcune misure molto accurate della posizione del pianeta Marte, e tali misure non andavano d'accordo né con la teoria di Tolomeo, né con quella di Copernico. Quando Tycho morì, Keplero si mise a studiare quelle osservazioni e cercò di interpretarle. Nel 1609, lo stesso magico anno in cui Galileo per primo puntò il telescopio verso il cielo, Keplero ebbe l'intuizione di quella che poteva essere la risposta al problema, e pubblicò le sue prime due leggi sui moti planetari:
Ciascuno di questi enunciati richiede qualche spiegazione. |
I successivi anni della vita di Keplero non furono troppo sereni. Il suo protettore, l'Imperatore Rodolfo, morì nel 1612, e anche se Keplero mantenne il suo incarico di matematico di corte e continuò a produrre importanti lavori, la sua vita fu sempre più rovinata dalla guerra. Si trattava della Guerra dei Trent'anni, un'aspra contesa religiosa che oppose Protestanti e Cattolici. La guerra iniziò a Praga nel 1618 e coinvolse tutta la regione dell'Europa di Keplero