#21c     Il volo verso Marte: un po' di calcoli

Notazioni varie e velocità di fuga

    Prima di iniziare, è opportuno stabilire le notazioni per le quantità che verranno considerate. Anche se alcune di esse sono di tipo vettoriale, ne verranno considerate solo le grandezze. Le notazioni in grassetto vengono usate soltanto per evidenziare meglio alcune quantità, ma non indicano mai il carattere vettoriale.

    Come in precedenza, r₁ = 1 UA è la distanza della Terra dal Sole, r₂ = 1,523691 UA quella di Marte, e (facendo una certa approssimazione) si assumerà che entrambi i pianeti si muovano su orbite circolari.

    La velocità V sarà misurata in chilometri al secondo (km/s), e le diverse velocità saranno contrassegnate con un indice. Le lettere v minuscole indicheranno le velocità associate alle orbite attorno alla Terra anziché attorno al Sole.

    Nella precedente sezione è stata già introdotta la velocità orbitale V₀ della Terra attorno al Sole, pari a circa 30 km/s (più precisamente 29,77 km/s), molto più grande di v₀ ~ 8 km/s (appross.) richiesta da un satellite per orbitare attorno alla Terra appena al di sopra della superficie (trascurando l'atmosfera!). Nella sezione 21 era stato notato che la velocità di fuga v_f  da una tale orbita bassa si ottiene moltiplicando v₀ per la radice quadrata di 2, pari a 1,41421356.... che approssimeremo qui a 1,414. Si ottiene così

    Un tale veicolo spaziale, tuttavia, non è ancora libero di muoversi verso ogni punto nello spazio. La velocità v_f  lo ha liberato dalla gravità terrestre, ma non dall'attrazione del Sole, attorno al quale continuerà a muoversi in un'orbita simile a quella terrestre, a circa V₀ = 30 km/s.

    La situazione è ora completamente analoga alla fuga da un'orbita bassa attorno alla Terra (solo che ora il costo è più alto!). Per liberarsi da un'orbita circolare attorno al Sole e lasciare il Sistema Solare, l'astronave deve lanciare i suoi razzi a una "seconda velocità di fuga"

    Per raggiungere V_f  il razzo deve in qualche modo aumentare la sua velocità di ulteriori 12,42 km/s, più di quanto non sia necessario per sfuggire alla gravità della Terra, partendo da uno stato di quiete sulla sua superficie! Per fortuna, esistono dei modi (discussi nella Sezione 35) di sfruttare il moto dei pianeti (o della Luna) per ottenere, almeno in parte, una tale spinta.

    Altre velocità che entrano nei calcoli sono la velocità V₁ con cui l'astronave parte dalle vicinanze della Terra per entrare nell'ellisse di Homann (a una distanza r₁ dal Sole), e la velocità V₂ con cui raggiunge l'orbita di Marte (a una distanza r₂). Inoltre, V₃ sarà la velocità di Marte nella sua orbita, assumendo che tale velocità abbia una grandezza costante (cioè assumendo che l'orbita di Marte sia circolare).

   Se V₂ > V₃, l'astronave sorpasserà Marte, mentre se V₂ < V₃ ne sarà sorpassata.

Equazioni richieste

    (1) Le leggi di Keplero

•     La prima legge dice che "I pianeti si muovono lungo ellissi, di cui il Sole occupa uno dei fuochi". Questa è stata già usata, infatti l'ellisse di trasferimento è una di tali orbite.

•     La seconda legge dice che "La linea che congiunge un pianeta al Sole spazza aree uguali in tempi uguali". Vediamo di estrarre da questa legge una equazione utile.

Applicazione della 2ª legge di Keplero

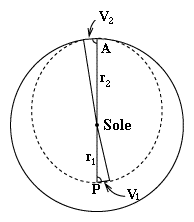
    Il disegno qui a fianco mostra l'orbita di Marte (linea continua) e l'ellisse di trasferimento (linea tratteggiata), con raggi (r₁, r₂) nei punti (perigeo, apogeo), a cui la velocità dell'astronave è (V₁, V₂). I piccoli segmenti disegnati in queste locazioni rappresentano la distanza percorsa dall'astronave durante il secondo successivo al passaggio per il perigeo o all'apogeo, e, per la definizione di velocità ("distanza percorsa durante un secondo"), queste distanze sono anche uguali a V₁ e V₂. In realtà, questi segmenti dovrebbero essere un po' incurvati come l'orbita, ma, data la loro piccola lunghezza, si può trascurare la differenza rispetto a segmenti di retta. Completiamo quindi i triangoli lunghi e sottili, che hanno come base queste linee.

    Notiamo che ciascuno di questi triangoli ha un angolo retto alla sua base, poiché all'apogeo e al perigeo (ma non in altri punti), la linea che va verso il Sole è perpendicolare all'orbita.

    Al perigeo, l'altezza del triangolo è r₁, la lunghezza della sua base è V₁, per cui dalla formula dell'area A₁ di un triangolo

    All'apogeo, l'altezza è r₂, la base V₂, e l'area è

    Ciascuno di questi triangoli viene "spazzato" in un secondo, per cui, dalla 2ª legge di Keplero, le loro aree devono essere uguali. Moltiplicando ambo i membri per 2 si ottiene

    Indichiamo con un numero questa equazione, per poterci riferire ad essa in seguito. Va notato che questa relazione vale soltanto al perigeo e all'apogeo. Negli altri punti dell'orbita, l'angolo tra il raggio vettore e l'orbita non è 90°, e anche l'area dipende dal suo esatto valore.

    La terza legge di Keplero era stata già usata per determinare il periodo orbitale. Ne avremo bisogno ancora alla fine.

   
(2) L'equazione dell'energia

    Nella sezione (12) si è detto che l'energia E di un satellite di massa m in orbita attorno alla Terra, in ogni punto della sua orbita, è

    Come si è notato prima, perché un oggetto in orbita attorno alla Terra possa sfuggire completamente alla gravità del Sole (ma soltanto appena appena!), occorre che abbia una velocità V_f = 1,414...×V₀ = 42,42 km/s. Sia E₀ l'energia di un tale oggetto. Allora, poiché

    Poiché possiede esattamente la velocità di fuga, se aspettiamo per un tempo lunghissimo, questo oggetto arriverà estremamente lontano dalla Terra, e, avendo praticamente esaurito tutta la sua energia cinetica, la sua velocità sarà molto prossima allo zero. Allora entrambi i termini a secondo membro dell'equazione (2) tenderanno a zero, per cui

    Dividendo per m e spostando il termine negativo V_f  a secondo membro

    da cui si può ricavare il valore di k

Un po' di calcoli

    Ritorniamo ora alla nostra astronave nella sua orbita di trasferimento verso Marte. La sua energia deve essere la stessa al perigeo P e all'apogeo A, per cui, dall'equazione (2)

    Dividendo ambo i membri per m ("eliminando m") e moltiplicandoli per 2

    Come primo passo, usiamo l'equazione (1) per esprimere V₂ :

    Sostituendo questa espressione a primo membro della (4)

    Questo può essere posto uguale al secondo membro della (4), e quindi abbiamo già un'equazione per il punto 2 della "ricetta" -- una sola equazione in una sola incognita, cioè V₁. Ma invece di procedere in modo troppo affrettato, è opportuno separare il maggior numero possibile di fattori. Forse qualcosa si potrà semplificare!

    Da una ben nota identità (ved. anche "Identità")

si ha             

    Conserviamo l'equazione (6) per un uso futuro e consideriamo il secondo membro della (4). Possiamo introdurvi un denominatore comune r₂:

    Per la (4), le espressioni (6) e (7) sono uguali:

    Il nostro trucchetto ha funzionato: ora entrambi i membri possono essere divisi per (r₂- r₁), si può eliminare quel termine e moltiplicare poi entrambi i membri per r₂ , ottenendo una ulteriore semplificazione. Se fossimo andati troppo di fretta poco fa, le nostre espressioni sarebbero state molto più complicate! Quello che resta è

    Moltiplicando per r₂, e dividendo per (r₂ + r₁), la quantità incognita resta isolata -- è al quadrato ma questo non importa:

    A questo punto sostituiamo i valori numerici:

    Possiamo estrarre la radice quadrata da entrambi i membri (una delle prime regole algebriche) e quindi

   
Se  V₀ = 30 km/s

e questo mostra che dobbiamo aggiungere soltanto 2,966 km/s, appena meno di 3 km/s pari al 10% della velocità orbitale.

L'arrivo vicino a Marte

    L'astronave ha ceduto un po' della sua energia cinetica per contrastare l'attrazione solare e spostarsi più lontano dal Sole. La questione importante è ora di confrontare questa velocità con quella V₃ di Marte sulla sua orbita.

    Per ricavare una velocità in km/s, le distanze devono essere espresse in chilometri e i tempi in secondi, ma "a beneficio dei principianti", suddividiamo il calcolo, evitando i numeri grandi e la notazione scientifica. Iniziamo con la 3ª legge di Keplero per orbite circolari, con la distanza r espressa in UA e il periodo orbitale T espresso in anni. Come si è visto nella precedente sezione (e anche nella sezione 10), con queste unità

    Per Marte:     r = 1,523691           T² = (1,523691)³ = 3,53745

Usiamo il valore numerico classico 1,8822 (poiché qui avavamo fatto alcune approssimazioni) e assumiamo 365,25 giorni per l'anno (giuliano). Si ha quindi:

    Durante questo tempo l'astronave percorre

    Dividendo per T, si ottiene

Ogni giorno ha (24)(3600) = 86400 secondi, per cui il tratto di orbita percorso da Marte ogni secondo è

    La "distanza-per-secondo" non è altro che la definizione di velocità. Pertanto

vediamo che è Marte quello che si muove più rapidamente, e sorpasserà l'astronave. Per accordare la sua velocità con quella di Marte, l'astronave dovrà generare una ulteriore spinta di 2,545 km/s.