| Newton ha dato la corretta risposta: oggetti più pesanti hanno un'inerzia maggiore. È vero che la palla da cannone è attratta verso il basso con una forza (diciamo) 10 volte più grande, però essa resiste all'accelerazione 10 volte più fortemente. Newton espresse questa spiegazione con una formula matematica -- "il secondo principio della dinamica", che è descritta in una prossima sezione. Comunque, in parole povere, il risultato è che entrambi gli oggetti cadono con la stessa velocità (trascurando la resistenza dell'aria). |
|
Questo discorso introduce un altro concetto, quello della massa di un oggetto, grossolanamente definita come la quantità di materia che esso contiene. L'inerzia è proporzionale alla massa, e anche il peso è proporzionale alla massa, per cui le due grandezze sono legate tra loro. La differenza è che l'inerzia è una proprietà inerente della materia, mentre il peso dipende dalla gravità. Una persona che pesa sulla Terra 60 chilogrammi, ne peserà soltanto 20 su Marte, e 10 sulla Luna.
Comunque il modo più facile e più comune di misurare la massa è quello di pesare un oggetto, usando quindi la gravità. In una bilancia a due piatti, si confronta il peso ignoto di un oggetto con quello di una serie di pesi noti. Pertanto la massa viene generalmente misurata in chilogrammi, anche se questi sono in realtà unità di peso. In una bilancia a un solo piatto, come quella in figura, il peso di confronto è fisso, ma facendolo scorrere a diverse distanze dal perno, si ottiene lo stesso risultato.
Come misurare la massa su una Stazione SpazialeNel 1973 la NASA mise in orbita la stazione spaziale Skylab, e tra i suoi esperimenti era compreso un accurato controllo della salute dell'equipaggio. Un parametro importante era la massa corporea degli astronauti. Qui sulla Terra si chiamerebbe "peso corporeo" e si misurerebbe pesando una persona su una bilancia. Tuttavia, le bilance non funzionerebbero su una stazione spaziale. Esse infatti usano la gravità, confrontando la forza di gravità esercitata sul corpo dell'astronauta con la tensione di una molla calibrata o con la forza di gravità esercitata su alcuni pesi calibrati. Non è corretto dire che la gravità non esiste su un veicolo spaziale in orbita (se non esistesse, il veicolo se ne volerebbe via senza più ritornare). Al contrario, nell'ambiente "a zero g" di una stazione spaziale, la gravità sta già facendo il suo dovere, mantenendo la stazione nella sua orbita, anche se all'interno della stazione questo non si nota. Poiché l'orbita è curva, il primo principio della dinamica non è violato, richiedendo una forza per mantenere quel tipo di moto. Come si può misurare la massa lassù? Ci possono dare un suggerimento gli orologi, i quali hanno bisogno di un qualche dispositivo per marcare il passaggio del tempo. Gli orologi a pendolo -- che devono stare sempre in posizione verticale -- usano la gravità, ma gli orologi da polso meccanici dipendono da un bilanciere, che ruota periodicamente avanti e indietro -- in senso orario, poi in senso antiorario, e poi di nuovo in senso orario -- sotto l'azione di una molla a spirale. In questo caso la gravità non c'entra. I moderni orologi da polso elettronici hanno sostituito il bilanciere con un cristallo di quarzo che vibra, che agisce un po' come un diapason: il movimento è molto più rapido, ma i circuiti a transistori riescono facilmente a tenere il conto delle vibrazioni, che sono estremamente stabili. |
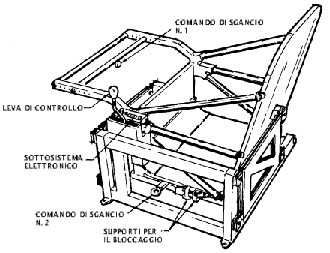 |
misurare la massa di un astronauta. |
|
...ed ora qualcosa di completamente diverso. Che dire se si potesse perdere peso senza perdere massa? Un secolo fa H.G. Wells scrisse uno spassoso ed umoristico racconto fantastico su questa possibilità, La verità su Pyecraft. Dateci un'occhiata!
|
Ulteriori dettagli: #17a Misure di massa a bordo della Stazione Spaziale Skylab
Il prossimo argomento: #18 Il secondo principio della dinamica
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 14 Agosto 2005