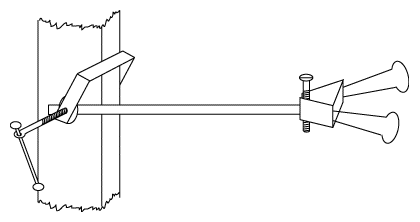
(la morsa è fissata alla zampa di un tavolo)
|
Con l'aiuto soltanto di semplicissime attrezzature, potrete effettuare una misura di massa simile a quelle eseguite a bordo dello Skylab.
|
Tutto quello di cui avete bisogno:
|
 |
(la morsa è fissata alla zampa di un tavolo) |
Istruzioni
|
|
Secondo la teoria, il periodo di oscillazione deve essere proporzionale alla radice quadrata della massa oscillante, inclusa la massa del ferma-fogli. Notate che la gravità non entra affatto in tutto questo: il periodo di oscillazione sarebbe lo stesso sulla Luna o in un ambiente a zero g. Si ottiene quindi
|
|
(T2/T1) = √(m2+m0)/√(m1+m0) = √[(m2+m0)/(m1+m0)].
|
|
("Il rapporto di due radici è uguale alla radice del rapporto dei radicandi"). Moltiplicando ogni membro per se stesso: (T2/T1)2 = (m2+m0)/(m1+m0). Se ci si trova nello spazio, dopo aver misurato T1 e T2, e conoscendo le masse m1 e m0, si può facilmente calcolare la massa incognita m2.
|
|
Pesi: m1 = 50 gr, m2 = 120 gr, m0 = 10 gr. Il numero di oscillazioni contate in un intervallo di tempo di 10 secondi era: con m1, 20 oscillazioni, con m2, 13,5 oscillazioni. Pertanto
|
|
T1 = 10 sec/20 = 0,5 sec T2 = 10 sec/13,5 = 0,74074 sec. da cui
(T2/T1)2 = 2,195 deve essere uguale a (m2+m0)/(m1+m0) = 130/60 = 2,167 |
|
L'accordo ottenuto con questi risultati è probabilmente migliore di quanto ci si potrebbe aspettare da un esperimento così grossolano, considerando il fatto che è stata trascurata la massa della lama da seghetto.
|
Il prossimo argomento: #18 Il secondo principio della dinamica
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 14 Agosto 2005