(24a)   La rotazione della Terra

Come la rotazione terrestre riduce la forza di gravità effettiva

    Tale velocità è diretta verso est ed è notevolmente maggiore della velocità del suono, che è di circa 335 m/s. I razzi lanciati da Cape Canaveral devono raggiungere 8 km/s (in un sistema di riferimento solidale con il centro della Terra non in rotazione) per poter entrare in orbita, per cui, per farli partire con una velocità iniziale favorevole, tali razzi vengono in genere lanciati verso est.

    Per ricavare la forza centrifuga all'equatore (cioè la forza espressa in newton che agisce su un grammo massa, in rotazione assieme alla Terra), la calcoliamo usando come unità i metri e i secondi

    Confrontando questo valore con l'accelerazione di gravità -- diciamo di 9,81 m/s² -- è soltanto 0,00346 o il 0,346%. L'effettiva gravità all'equatore è ridotta dalla rotazione, ma soltanto di circa 1/3 per cento.

Il rigonfiamento terrestre all'equatore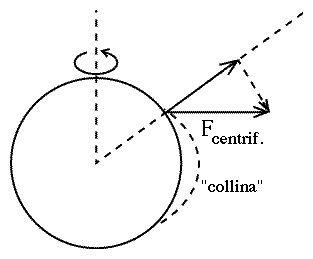

    Supponendo che la Terra sia esattamente sferica, ci aspetteremmo che la forza di gravità sia sempre diretta verso il centro della Terra. Tuttavia, la forza centrifuga è perpendicolare all'asse della Terra. Tranne che all'equatore, quindi, questa forza non è esattamente orientata in direzione opposta alla gravità, ma vi è una piccola componente vettoriale in direzione orizzontale, diretta verso l'equatore (ved. la freccia tratteggiata nel disegno). Come conseguenza, non solo la forza di gravità effettiva viene indebolita, ma viene anche modificata la sua direzione -- invece di essere diretta verso il centro della Terra, è un po' inclinata (anche se molto poco) verso l'equatore.

    Forse che questo significa che, se si appoggiasse una palla da biliardo perfetta su una superficie orizzontale liscia e senza attriti, la gravità la farebbe rotolare verso l'equatore...? Supponiamo che sia così. Questa stessa forza agirebbe anche sull'acqua degli oceani e li farebbe fluire verso l'equatore, e anche la Terra solida verrebbe deformata!

    Per quanto tempo durerebbe questo effetto? Bene, finché l'accumulo di materiale nella zona equatoriale non abbia formato intorno alla Terra una specie di "collina", che si sollevi leggermente verso l'equatore, dove si troverebbe la sua sommità. Non vi sarebbe più flusso di materiale verso l'equatore il momento in cui la pendenza del suolo, modificato dalla formazione della collina, venisse ad essere esattamente perpendicolare all'effettiva direzione (modificata) della forza di gravità. Con una tale pendenza, una palla da biliardo perfetta posta su una superficie perfettamente orizzontale non rotolerebbe più da alcuna parte, e le forze sugli oceani e sul terreno non cercherebbero più di spostare la materia orizzontalmente.

    Ma adesso vi dovreste rendere conto di dove siamo arrivati con queste ipotesi: ad una spiegazione del rigonfiamento equatoriale della Terra! Il rigonfiamento non è altro che la "collina" descritta poco fa, e la forma della superficie è tale che il terreno è sempre perpendicolare all'effettiva forza di gravità.

    Giove ruota su se stesso in meno di 10 ore e ha un raggio equatoriale circa 11 volte quello della Terra, generando quindi una forza centrifuga molto più intensa. Come conseguenza, nonostante la sua gravità superficiale sia 2,64 volte quella sulla Terra, Giove è molto più rigonfio all'equatore, di circa il 6,5%. La forma schiacciata di Giove fu notata al telescopio da Giovanni Cassini (1625-1712), direttore dell'Osservatorio di Parigi. Tuttavia lui e suo figlio sostenevano che la Terra era diversa, che cioè fosse rigonfia ai poli (più simile a un limone che a un pompelmo). Essi basavano le loro affermazioni sulle misure fatte al suolo, secondo le quali sembrava che le linee di latitudine si facessero più vicine tra loro all'avvicinarsi al polo.

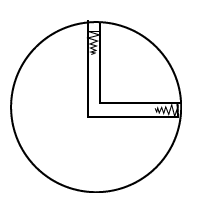
    Le loro affermazioni furono in seguito smentite da osservazioni più accurate, ma ancora prima, Newton con la seguente semplice argomentazione dimostrò che non poteva essere così. Supponiamo che la Terra sia sferica, e immaginiamo due profondi fori che arrivino fino al suo centro (ved. figura), e lì si incontrino. Riempiamoli poi di acqua. Se la Terra non ruotasse, ci si potrebbe aspettare che l'altezza di ciascuna delle due colonne d'acqua sia la stessa: al centro della Terra, per simmetria, ogni colonna preme in giù con lo stesso peso, producendo un equilibrio.

    Quando la Terra ruota, tuttavia, l'azione della forza centrifuga riduce il peso dell'acqua nel foro equatoriale, e quindi lì l'acqua salirebbe ad una altezza maggiore. Newton pertanto concluse che in ogni punto l'acqua sarebbe salita allo stesso livello
 

    Per altre informazioni sul rigonfiamento terrestre (inclusa una trattazione matematica più avanzata) si può visitare il sito Web "The Bulging Earth" (Il rigonfiamento della Terra).

Un aviogetto al di sopra dell'equatore

    La forza centrifuga è un concetto utile per analizzare le condizioni di equilibrio in un sistema di riferimento in rotazione, nei casi in cui le forze si controbilanciano esattamente e non vi è alcun moto.

    Calcolare il moto in un sistema di riferimento rotante è molto più complicato, e in genere va oltre il livello di questa trattazione. Tutto ciò che è esposto in questa sezione e in quella seguente serve a mettere in luce queste complicazioni.

    Supponiamo che la riduzione della gravità effettiva sia la stessa anche alla quota di volo di un aereo di linea -- esiste in realtà una piccola differenza, ma non influisce sull'argomento trattato qui di seguito. Due aviogetti volano lungo l'equatore a uguale velocità -- uno verso est e l'altro verso ovest. Poiché essi volano in cerchio attorno al centro della Terra, la gravità effettiva a bordo di ciascuno è un po' variata. La variazione è la stessa per entrambi?

Potreste pensare di sì, ma non è vero.

    Sarebbe la stessa se la Terra non ruotasse (trascurando qui l'attrazione solare e la rivoluzione della Terra attorno al Sole, due effetti che pressoché si bilanciano). Senza la rotazione terrestre, nel sistema di riferimento dell'universo, il moto verso est e il moto verso ovest sarebbero completamente simmetrici.

    In realtà, tuttavia, le velocità dei due aviogetti sono misurate relativamente all'atmosfera, la quale anch'essa ruota attorno al centro della Terra. Vista dal sistema di riferimento dell'universo, la velocità dell'aviogetto che vola verso est si somma alla rotazione dell'atmosfera, mentre quella dell'aereo che vola verso ovest viene sottratta.

    Supponiamo che si tratti di due aerei supersonici, come il Concorde, che volano a 465,1 metri/sec. Piuttosto che studiare il moto in un sistema di riferimento rotante, che potrebbe dare o non dare una risposta corretta, torniamo sempre al sistema di riferimento, non in rotazione, dell'universo. In tale sistema di riferimento, la velocità di rotazione dell'aereo che vola verso ovest è zero, e quindi l'aereo non risente di una riduzione della gravità effettiva. Nello stesso riferimento, l'aereo che vola verso est ha una velocità doppia, e poiché la forza centrifuga è proporzionale al quadrato della velocità (v²), l'aereo percepisce una forza centrifuga quattro volte maggiore. La gravità effettiva a bordo di questo aereo è ridotta di quattro volte rispetto alla riduzione percepita al suolo, cioè dell'1,384%.

Che cosa significa

    Il primo principio della dinamica (o prima legge di Newton) certamente non vale -- un corpo su cui non si esercita alcuna forza non rimarrà in quiete, ma volerà via per la tangente. Si può cercare di rappezzare questa legge aggiungendo una forza centrifuga in ogni calcolo in cui si debbano equilibrare delle forze. Ma se tali forze non sono in equilibrio, se esse causano un moto nel riferimento rotante, allora occorre usare una forma modificata delle leggi di Newton. Tale forma modificata esiste, ma va al di là del livello di questo corso. L'esempio riportato suggerisce l'esistenza di alcuni problemi connessi con i riferimenti rotanti, ed altri esempi si trovano nella sezione successiva, dove si parla dell'effetto di Coriolis.

    Voi ed io (oltre a chiunque altro si trovi sulla Terra) viviamo in un sistema di riferimento in rotazione. Dovremmo allora rinunciare ad usare le equazioni di Newton, nella vita di tutti i giorni? Fortunatamente, per moti su una scala molto minore delle dimensioni della Terra, a velocità moderate, gli effetti sono trascurabili.

    Un esempio riguarda la famosa domanda se l'acqua che va giù nel lavandino in località a nord e a sud dell'equatore ruoti in direzioni opposte, come talvolta viene affermato. Effettivamente (come si vedrà nella prossima sezione) questo fenomeno in linea di principio esiste, ma è troppo esiguo per poter essere osservato. Nel romanzo "La Guerra dei Mondi", i cannonieri che sparavano con i grossi cannoni verso la Terra correggevano (leggermente) il tiro per tener conto della rotazione terrestre, ma noi potremo generalmente ignorare l'effetto, tranne che per la variazione della gravità dovuta alla forza centrifuga.