La terza legge di Keplero consente di valutare le dimensioni del Sistema Solare in unità di misura relative, per esempio in "unità astronomiche" (UA), dove 1 UA è la distanza media Terra-Sole. Tuttavia, per esprimere l'UA in chilometri o in miglia, occorre una qualche sorta di parallasse, cioè qualche differenza nella posizione osservata di un oggetto del Sistema Solare, quando venga visto da due punti diversi, di cui sia nota la distanza (in chilometri o in miglia). Il problema è che gli oggetti planetari sono enormemente lontani, per cui lo spostamento della loro posizione apparente, quando li si osservi da due località diverse della Terra, è piccolissimo. Edmond Halley propose di usare il transito di Venere sul disco solare, quando il pianeta appare come un cerchietto scuro -- per citare un osservatore del transito avvenuto nel 2004, come "un mirtillo davanti a una grossa arancia". Questo tipo di evento è piuttosto raro. I transiti avvengono a coppie di date ravvicinate, che però si ripetono a distanza di più di un secolo: nel XX secolo non vi sono stati transiti, mentre uno ne è avvenuto nel 2004 e un altro si verificherà nel 2012.
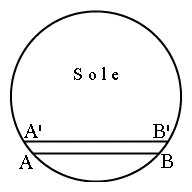
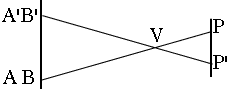
Supponiamo che un osservatore nel punto P sulla Terra veda Venere passare davanti al disco solare da A a B (ved. Figura 2 qui sopra, le due immagini sono una di fronte e una di profilo). Il moto di Venere attraverso il disco solare è dovuto alla combinazione del moto orbitale dei due pianeti. Per le leggi di Keplero, più il pianeta è vicino al Sole, e più si muove rapidamente, per cui Venere si muove più velocemente della Terra, e durante il transito la sorpassa. Il piano dell'orbita di Venere è molto prossimo al piano dell'orbita terrestre, noto in genere come il piano dell'eclittica (prossimo ma non coincidente, altrimenti avverrebbe un transito ogni volta che Venere sorpassa la Terra). Pertanto sulla sfera celeste la linea AB è quasi parallela alla linea dell'eclittica, cioè la linea lungo cui il piano dell'eclittica interseca la volta celeste. Vista da un diverso punto di osservazione P', Venere si muove lungo A'B', praticamente parallela ad AB. E' preferibile che quest'altro punto si trovi sul lato opposto dell'equatore, in modo che sarà probabile che si trovi anche sul lato opposto dell'eclittica. Se ora misuriamo la distanza D tra AB e A'B', possiamo, in linea di principio, applicare qualche semplice nozione di trigonometria alla parallasse e ricavare la distanza PV tra P e la posizione V di Venere. Magari l'astronomia fosse così semplice! In realtà, le linee AB e A'B' sono estremamente vicine tra loro. La figura all'inizio della pagina (la foto originale è su questo sito) mostra le immagini di Venere davanti al disco solare, ottenute l'8 giugno 2004 da 3 località diverse, e ciascuna serie di immagini è indicata con un diverso colore. E' evidente che i percorsi sono molto vicini, più vicini del diametro del dischetto di Venere. Dalla misura separata di ciascuna serie di dati e dal calcolo della loro separazione D, non si può certo pensare di ottenere un risultato molto preciso. Quello che Halley notò era che un'informazione equivalente si poteva ottenere cronometrando il passaggio di Venere da A a B e da A' a B'. Poiché il bordo del Sole si incurva, la lunghezza del segmento AB è diversa dalla lunghezza di A'B' (parliamo di "lunghezza" per semplicità -- in realtà AB, A'B' e D sono tutti angoli sotto cui l'osservatore vede le lunghezze). La velocità apparente del moto di Venere sul disco solare è quasi la stessa quando l'osservazione sia fatta da località diverse sulla Terra, per cui, misurando la differenza temporale tra i passaggi AB e A'B', si può ricavare la distanza D. Questa misura è molto più agevole poiché il transito dura ore, e la differenza tra i tempi di transito può essere di qualche minuto. Pertanto queste durate si possono misurare (in linea di principio) piuttosto accuratamente. In queste 3 sezioni illustreremo un procedimento semplificato per ricavare l'unità astronomica dai tempi di transito dell'8 giugno 2004, usando le durate previste per i transiti. Gli astronomi che hanno calcolato queste durate (disponibili su questo sito Web) hanno usato naturalmente un valore ben consolidato dell'unità astronomica, per cui questo è soltanto un esercizio. Se questo fosse stato un "reale" calcolo, si sarebbero dovuti usare dati ottenuti da osservazioni. Si tratta qui di un calcolo un po' grossolano, svolto usando molte approssimazioni e trascurando delle correzioni che sarebbero necessarie in un calcolo effettivo.
Poiché siamo liberi di scegliere le stazioni di osservazione, ne abbiamo scelte due quasi sulla stessa longitudine e a latitudini uguali a nord e a sud dell'equatore. Entrambe sono in Africa (latitudine e longitudine sono approssimate entro circa mezzo grado).
Questa simmetria delle posizioni semplifica il procedimento. Come si è già fatto notare, il moto di Venere sul disco solare è quasi completamente dovuto al moto orbitale della Terra e di Venere. Con la Terra che orbita attorno al Sole a 30 km/s, si potrebbe pensare che la velocità dovuta alla rotazione terrestre dia un contributo trascurabile, poiché si tratta soltanto di un centinaio di metri al secondo. Tuttavia, questa velocità fa spostare la posizione dell'osservatore durante il transito, che si svolge in più di 5 ore. Durante un tempo così lungo, un osservatore si può essere spostato anche di un tratto pari a un raggio terrestre, e la differenza di spostamento di due osservatori a diverse latitudini può raggiungere varie migliaia di chilometri. D'altra parte, l'informazione da cui si vuole ricavare l'unità astronomica è contenuta in una differenza temporale ΔT di soli 5 o 6 minuti, durante i quali la Terra si muove di circa
Uno spostamento aggiuntivo di qualche migliaio di chilometri potrebbe seriamente degradare il risultato, rendendo necessaria una ulteriore correzione. Per semplificare il calcolo svolto qui, abbiamo aggirato il problema scegliendo due località poste alla stessa distanza dall'equatore, e quindi con identiche velocità di rotazione. Scegliendo inoltre anche la stessa longitudine, si equalizzano le velocità rispetto a Venere e al Sole. Pertanto le durate di entrambi i transiti sono influenzate allo stesso modo, e si potrà quindi usare ΔT senza ulteriori correzioni. Questa pagina Web è collegata ad altre due pagine. La prossima pagina mostra il modo di derivare D. Il calcolo richiede un po' di trigonometria trattata nel "ripasso di matematica" e in particolare le formule per il seno e il coseno della somma di due angoli, discusse nella sezione M-11. Nella pagina successiva viene poi ricavato un valore approssimato dell'unità astronomica. A causa delle approssimazioni usate, il risultato sarà inesatto di qualche percento, tuttavia il procedimento non richiede particolari cognizioni di matematica oltre quelle usate fin qui. Verranno anche evidenziate alcune complicazioni con cui gli astronomi professionisti devono in genere confrontarsi. Un archivio fotografico del transito (inclusa una immagine presa da un aereo in volo). Si può fare clic qui per una vasta serie di collegamenti relativi al transito di Venere.
|