|
Questa pagina è la continuazione de Il Transito di Venere--Introduzione, e usa le stesse notazioni.
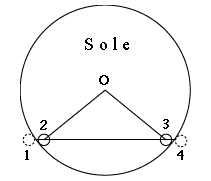
Le previsioni per il transito dànno quattro tempi di "contatto", cioè gli istanti in cui il dischetto nero di Venere tocca il bordo del disco solare (indicati dai numeri nella Figura 3).
Ovviamente, Venere non è visibile durante il primo e il quarto contatto, per cui usiamo il secondo contatto per definire A o A', e il terzo contatto per definire B o B' (ved. Figura della pagina precedente, citata sopra). Il disco del Sole ha un diametro apparente 2R di circa 31.5 minuti d'arco, e il raggio r di Venere è di circa 1 minuto d'arco. Come si è notato per AB, ecc. sulla pagina prcedente, R e r non sono distanze ma angoli, anche se in questi calcoli tutti gli angoli sono stati considerati come distanze, trattandosi di valori molto piccoli. Si può immaginare la Figura 3 proiettata sull'interno di una grande sfera (p. es. la cupola di un planetario, o anche la sfera celeste stessa). Un'area di mezzo grado, che è approssimativamente il diametro angolare del Sole, copre una parte così piccola dell'intera sfera, che - con buona approssimazione - si può considerare piatta, e le distanze su tale sfera sono praticamente proporzionali all'angolo coperto. Poniamo i punti A e B, non situati sul bordo del disco solare durante il secondo e il terzo contatto, ma nel centro del dischetto di Venere in quegli istanti. Se indichiamo con O il centro del Sole, questi punti si troveranno disposti su una circonferenza di centro O e di raggio (R–r). Pertanto, il tempo impiegato a percorrere AB corrisponde al passaggio di Venere su una corda (cioè un segmento che taglia la circonferenza) di un "Sole ridotto", che copre un angolo di soli 30.5 minuti d'arco.
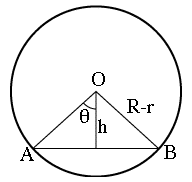
Ci occorre anche un valore abbastanza accurato della distanza h della linea AB dal centro O, o meglio ancora l'angolo θ (theta, ved. Fig. 4 qui in basso), che è la metà dell'angolo sotteso da AB. Derivandolo dalle fotografie pubblicate (p. es. la versione disponibile sul Web della Fig. 1 della pagina precedente, oppure grafici forniti dall'Univ. del
Lancashire) si ottiene un valore di circa 46.4 gradi. Allora (ved. la Figura 4 qui sotto)
Poiché il tempo di transito T è proporzionale alla distanza (AB), possiamo scrivere
dove k è un fattore di proporzionalità. La conoscenza del suo valore non è necessaria, poiché il nostro obiettivo è quello di usare il rapporto tra T e la differenza ΔT dei tempi di transito osservati in due diverse località, e in tale rapporto il fattore k si elimina. Usando la trigonometria
Se la linea A'B' osservata dall'altra località è leggermente più lunga, essa sottenderà un angolo leggermente più grande 2(θ+δ), e la sua distanza da O non sarà h ma = (R–r)(cosθ cosδ – sinθ sinδ ) (3) Se δ è un angolo molto piccolo, anche sinδ è molto piccolo. Ma anche se un valore piccolo di sinδ resta ancora significativo, per essere incluso nei calcoli, cosδ è probabilmente così vicino a 1, che si può tranquillamente sostituire con 1. Per dimostrarlo, notiamo che Ricordando che una radice quadrata equivale alla potenza (1/2), dal teorema binomiale Pertanto, se approssimiamo cosδ con 1, l'errore commesso è solo dell'ordine di sin2δ, che (come avviene per i numeri piccoli) è molto più piccolo di sinδ. Se, per esprimere h', conserviamo sinδ ma sostituiamo cosδ con 1, si ottiene con buona approssimazione da cui Il tempo di transito nel punto P' si ottiene in modo simile all'equazione (2) = 2k (R–r)(sinθ cosδ + cosθ sinδ) e con la stessa buona approssimazione usata prima, con l'angolo δ piccolo
E quindi = cosθ sinδ / sin θ (6) Come si poteva prevedere, la piccolezza del rapporto a primo membro è bilanciato dalla piccolezza di sinδ a secondo membro. Risolvendo rispetto a sinδ Questo valore può essere sostituito nell'equazione (4) che fornisce D, un altro termine molto piccolo Questo è quanto ci serviva. Come Halley aveva indicato, lo spostamento D tra i percorsi del transito di Venere è ora espresso in funzione della differenza osservata tra i tempi di transito, come pure della lunghezza del tempo di transito osservato T (o della sua media (T + T')/2) e dell'angolo θ, che corrisponde alla distanza del percorso del transito dal centro del Sole. |