Mapa del sitio

(22a) La Aberración de la Luz Estelar

Nota: En esta sección, las cifras vectoriales se escriben en negrita. 

Imagínese a si mismo sentado en una embarcación, viajando sobre el agua con una velocidad "u" en un día de calma. Una pequeña bandera está atada al mástil: ¿Hacia qué dirección apuntará?
Mirando desde la embarcación, la bandera siempre apunta hacia atrás, porque en el marco de referencia de la embarcación, parece que sopla un viento de velocidad -u. Siempre apunta a la misma dirección. 

¿Qué pasa si el día no está en calma? ¿Si sopla un viento con velocidad v? En el marco de referencia de la embarcación, el aire ahora se mueve con una velocidad de v - u , un vector suma, con la dirección de v especificada relativa a la embarcación ("en el marco de la embarcación"). La bandera ahora ni apunta a favor del viento, ni en dirección hacia atrás, sino hacia algún sitio entre ambos. 

Suponga que la embarcación ahora cambia de dirección. En el marco de referencia de la embarcación u está aún dirigiéndose hacia atrás, pero el viento ahora parece que llega desde una dirección diferente, relativa a la embarcación. Consecuentemente, la dirección de v cambia, y la bandera, apuntando hacia la nueva v - u, asimismo tiene una dirección diferente. 
 

El Desplazamiento Aparente de las Estrellas

Esta sección trata de la luz estelar, no de embarcaciones y banderas. Desde la época de Newton, los astrónomos han intentado conocer lo lejos que estaban las estrellas mediante el método del paralaje, usando el diámetro de la órbita de la Tierra como base. De forma cuidadosa medían las posiciones de las estrellas en fechas separadas por medio año, representando dos posiciones de la Tierra separadas 300,000,000 km, y luego comprobaban si las posiciones de las estrellas en el cielo habían cambiado. Pronto encontraron que, efectivamente, las posiciones cambiaban. El problema era que las observaciones no tenían mucho sentido.
Jean Picard, uno de los antiguos astrónomos franceses, hizo posible observaciones más precisas introduciendo un visor en la lente del telescopio. Con este instrumento observó, hacia 1680, que las posiciones observadas de las estrellas no eran siempre las mismas. John Flamsteed, el astrónomo real de Inglaterra, principal del Royal Observatory en Greenwich, confirmó esos cambios. Por ejemplo, la Polar parecía viajar anualmente alrededor de un círculo de un radio de 20" ( 20 segundos de arco). 

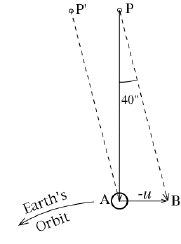
Como se planteó en la sección sobre el paralaje, el diámetro de ese círculo (40") podría sugerir que la distancia a la Polar era 1/40 de parsec o menos de 0.1 año luz. Sin embargo, los cambios en la posición no ocurrían en los momentos esperados. El mayor cambio de la Polar en cualquier dirección no ocurría cuando la Tierra estaba en el final opuesto de su órbita, como debería ser, sino 3 mese más tarde. 

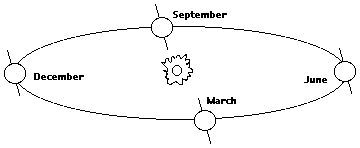
 Por ejemplo, en el dibujo superior, la posición aparente de la Polar se debería haber movido lo más lejos en la dirección de "Diciembre" cuando la Tierra estuviera en "Junio", que es lo más lejos que puede ir en la dirección opuesta. En lugar de eso, ocurría en Setiembre, cuando la Tierra se había movido 90º desde su posición de Junio. En verdad, el dato importante no era el desplazamiento de la Tierra, sino su velocidad, que en Setiembre apuntaba hacia la dirección hacia la que se desplazaba la Polar. 
 

Aclaración de Bradley

Los astrónomos estaban muy perplejos, más aún cuando se dieron cuenta de que todas las estrellas cercanas a la Polar cambiaban de igual forma. En el año1729, el astrónomo real británico, James Bradley, hizo un viaje en barco sobre el río Támesis, cerca de Londres, y observó un comportamiento raro en la bandera del tope del mástil: no apuntaba a favor del viento ni hacia la popa del barco, sino hacia una dirección entre ambas y cuando el barco cambiaba de rumbo, esa dirección también cambiaba. 
A Bradley le sobrevino una inspiración repentina. La bandera percibía la combinación de dos flujos de aire, tal y como se sentían en el marco del barco: un flujo debido al viento, el otro debido al movimiento del barco. De forma similar, razonó que la velocidad de la luz que llegaba de la Polar estaba modificada por nuestro propio marco de referencia, !Sumándole la velocidad de la Tierra¡ 

La velocidad de la luz, denominada universalmente por la letra c, como en        "E = mc2", fue calculada en el año1675 por Ole Romer, un danés que trabajaba en el observatorio de París, a partir de un estudio de los eclipses de una luna de Júpiter. La velocidad u de la Tierra en su órbita también era conocida. Visto desde el marco de la Tierra en movimiento, el resto del Universo tiene una velocidad -u, perpendicular a la velocidad c de la luz que llega de la Polar. Sume las dos, como vectores y obtendrá el desplazamiento observado. 

    [Puede muy bien preguntarse: ¿cuando sumamos u y cuando (-u)? 
       Cuando estamos en el exterior y observamos un objeto moviéndose con velocidad u, p.e. un avión con viento lateral,  sumamos u  a sus otros movimientos. 
        Pero cuando u es la velocidad con la cual nos movemos nosotros los observadores, el mundo exterior se está moviendo en relación a nosotros con una velocidad (-u). Luego (-u) deberá sumarse a cualquier otro movimiento observado en el mundo exterior.]
    Hoy en día somos muy conscientes de que sumarle -u a la velocidad de la luz estelar en, en principio incorrecto: cuando se suman velocidades cercanas a c, se deben usar las fórmulas de la teoría de la relatividad de Einstein. Si sumamos -u a c en la forma habitual, obtendremos una velocidad mayor que c, mientras que, en la teoría de la relatividad, la velocidad de la luz es siempre c, independiente de como se observa. Sin embargo, deducimos que el desplazamiento de la dirección calculada por Bradley es la misma que la que nos daría la relatividad. 

    Déjenme calcular aquí, a la manera que quizá lo hizo Bradley, ignorando la relatividad y usando la misma "pre-trigonometría" introducida en la sección del paralaje. 

    En el dibujo mostrado aquí, hacemos a AP la dirección hacia la Polar, la estrella está mucho más distante, y AB está junto con -u, opuesta al movimiento de la Tierra. Para simplificar el cálculo asumiremos que AP es perpendicular a AB. (Realmente el ángulo entre las dos es pequeño, requiriendo una corrección y haciendo que el movimiento aparente no sea un círculo, sino una elipse.)

 

El vector PA representará c, la velocidad de la luz proveniente de la Polar a c=300,000 km/s, mientras que AB es la velocidad (-u) sumada a c, de magnitud 30 km/s. La longitud de cada lado del triángulo ABP es proporcional a la velocidad que representa , de tal forma que ese triángulo se ve como la rebanada de un círculo y el ángulo en P se denomina por a, tenemos 

30/(2p 30,000) = 30/60,000p = a/360° 

a= 10800/60000p = 5.7296/1000 grados. 

Cada grado tiene 60 minutos de arco (60') y cada minuto tiene 60 segundos de arco (60"), unidades que no están relacionadas a los minutos y segundos de tiempo. Así, cada grado equivale 3600", dando 

a = 3600" (5.7296/1000) = 20.6" 

Medio año más tarde la dirección de u se invierte y el desplazamiento es en la dirección opuesta, dando un rango anual de unos 40", como lo observado. 
 

Aberración del Viento Solar

Un proceso algo similar se evidencia en el viento solar, una rápida emisión (~400 km/s) de gas caliente desde el Sol. Se origina en la corona solar, la capa más alta y más enrarecida de la atmósfera solar. Esta capa es tan caliente (aprox.1,000,000° C) que no consigue un equilibrio estático estable, sino que mana hacia afuera en un constante flujo de gas caliente y rarificado. 
Hablando con rigor, el viento solar es un plasma, una mezcla de electrones e iones positivos libres, átomos que han perdido electrones en las violentas colisiones que ocurren en un gas a 1,000,000 ºC. Siendo un plasma, puede conducir corrientes eléctricas y sus partículas pueden ser dirigidas por campos magnéticos. El magnetismo terrestre, en particular, desvía el flujo de viento solar, creando una cavidad alargada conocida como magnetosfera, de la que se excluye el viento solar (vea la figura). En el lado que da al Sol, el viento solo alcanza 10-11 radios terrestres (65-70,000 km.) antes de ser desviado lateralmente. En el lado nocturno, el que no mira hacia el Sol, una larga "cola magnética" se extiende a gran distancia, a lo largo de la dirección del flujo del viento solar. 

Pero, ¿cual es esa dirección? En el marco de referencia del Sol, el viento solar, por término medio, fluye radialmente hacia afuera, con una velocidad v de unos 400 km/s (que no cambia con la distancia). La Tierra, sin embargo, orbita el Sol con una velocidad u perpendicular a v de unos 30 km/s. Visto desde el marco de referencia de la Tierra, se añade a v una velocidad -u, de tal modo que para nosotros el viento solar parece que se mueve con v' = v - u, como indica el dibujo. La magnitud v' de la nueva velocidad se calcula aplicando el teorema de Pitágoras al triángulo ABC, que da 

(v')2 = v2 + u2     v' = 401.12 km/s

Si b es el ángulo con el cual  se mueve el viento solar en el marco de la Tierra, tenemos 
 
sen b = 30/401.12 = 0.0749         (o bien, tan b = 30/400 = 0.075) 
          b = 4.289° 

 Con una astronave que explore la distante cola del lado nocturno, como hizo la japonesa "Geotail"  (a distancias de unos 200 radios terrestres), este efecto debe tenerse en cuenta si queremos poner la nave en la cola y no cerca de ella. Desafortunadamente, la dirección de v también varía de forma aleatoria varios grados, así que tener en cuenta  b ayuda, pero algunas veces un punto que se calcula para estar dentro de la cola no se halla en ella. 
 

Penachos de Humo

Un barco de vapor se mueve a través del océano con una velocidad u ycon una velocidad de viento v perpendicular a u. Si u define el eje de las x y v el de las y, ¿en qué dirección queda rezagado el penacho de humo detrás del barco? 
Este problema es mucha más fácil si trabajamos en el marco de referencia del barco. En ese marco, y en ausencia de viento, la velocidad del humo es -u. Sumando el viento al movimiento, la velocidad del humo se convierte en v-u       ( = v + (-u)), y ese vector define la dirección del penacho de humo rezagándose tras del barco. Deberá estar en el cuarto (-x,y) del plano de coordenadas, y el ángulo entre él y el eje (-x) satisface 

tan a = v/u         o bien  sen a = v/w,  w = u + v

Intentar resolver este problema en el marco de referencia del océano donde se mueve el barco puede resultar confuso, porque no estamos sumando las velocidades, sino los desplazamientos. Después de que se libera cada soplo de humo, ya no comparte la velocidad del barco. Solo en el marco de referencia del barco se hacen los movimientos más simples . 

 

Colas de Cometas y la Sonda Solar

En lugares cerca del Sol, pueden ocurrir mayores aberraciones, ya que los objetos aumentan su velocidad cuando se aproximan al Sol ( vea la 2ª ley de Kepler ). Esto tiene un interesante efecto en la cola de los cometas, las cuales actúan parecido a los penachos del ejemplo precedente. 
Normalmente un cometa, con un diámetro de 1-20 km, es una mezcla de gases congelados y polvo (una "sucia bola de nieve") que estaba amontonado en el exterior, que alcanza el sistema solar, y es atraído a una órbita hacia el Sol. Cuando el cometa se aproxima al Sol, sus gases congelados se evaporan por el calor y se forma su larga cola, empujada fuera del Sol por la luz y el viento solar. Así, la cola apunta hacia atrás del cometa cuando se acerca al Sol, pero lo hace hacia adelante cuando se aleja de nuevo. 

Realmente se observan a menudo dos colas distintas, una cola de polvo empujada por la presión de la luz solar, y una cola de plasma empujada por el campo magnético del viento solar (son raras las colisiones directas entre las partículas del cometa y del viento solar). Los colores de las dos colas son diferentes: en el cometa Hale-Bopp en 1997 (vea imagen) la cola de plasma era azul, un color producido por los iones que lo forman, mientras que la cola de polvo era blanca, el color de la luz solar dispersa. 

La cola de polvo apuntaba en la dirección de la luz solar, como se observaba desde el cometa: probablemente cambiaba como la luz observada por Bradley, pero en un ángulo muy pequeño para percibirse con la vista. La cola de plasma, por otro lado, apuntaba en la dirección del viento solar, de nuevo como se percibía por el cometa. Como vimos arriba, la Tierra ve el viento solar movido unos 4º, pero para el cometa el corrimiento es apreciablemente más grande, porque se mueve más rápido que la Tierra, especialmente cuando está más cerca del Sol. Las dos colas, por lo tanto, forman un ángulo distinto, como se ve en la figura. 

Un efecto aún mayor de aberración se prevé abordo de la sonda solar, prevista por la NASA para la observación del viento solar cerca del Sol. Esta nave espacial se espera que se aproxime al Sol hasta los 4 radios solares, evitando el fundirse por el intenso calor protegiéndola detrás de un escudo protector diseñado especialmente. 

Uno puede preguntarse, ¿como puede entonces cubrirse de la luz del Sol y observar el viento solar, que, al igual que la luz fluye hacia fuera de forma radial? En eso es en lo que ayuda la aberración. En el acercamiento máximo (perihelio) la sonda solar se moverá a unos 300 km/s, así que el viento solar, que se mueve a 400 km/s (pero no la luz solar) sufrirá una aberración de unos 37°, permitiendo alcanzar los detectores protegidos dentro del escudo de calor. 
 

Página principal en Español (índice)


Linea del Tiempo               Glosario .

Opcional: #22b La Teoría de la Relatividad

Próxima Etapa: #22c El vuelo del Aeroplano

Author and Curator:   Dr. David P. Stern
     Messages to Dr.Stern:   stargaze("at" symbol)phy6.org   (English, please) .

Spanish translation by J. Méndez

Last updated 13 December 2001