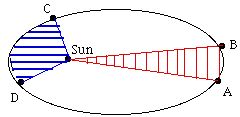
La LeyLa elipse trazada por un planeta alrededor del Sol tiene una forma simétrica, pero el movimiento no es simétrico. Piense en una piedra lanzada hacia arriba: cuando sube pierde velocidad, durante un instante, en la cima de su trayectoria, se mueve muy despacio y finalmente cae, aumentando su velocidad de nuevo. El movimiento de un planeta alrededor del Sol o el de un satélite científico alrededor de la Tierra, siguen ecuaciones diferentes (aunque existe alguna unión), pero en muchos aspectos se parecen al de la piedra. Esto es mucho más evidente si su órbita es alargada, o sea, si su excentricidad es casi 1. Cuando el planeta o el satélite se eleva en su órbita, su velocidad disminuye y cuando retorna, se acelera de nuevo, moviéndose a su mayor velocidad cuando está más cercano. Este punto de la órbita se llama perihelio para un planeta ("helios" es el Sol) y perigeo para un satélite terrestre ( "geo", es relacionado con la Tierra). Después de estudiar observaciones reales, principalmente de Marte, Kepler propuso la siguiente regla para predecir la aceleración y la deceleración. Dibuje una línea ("radio vector") desde el centro del Sol hasta el planeta (o desde el centro de la Tierra hasta el satélite). La ley de Kepler afirma que: "El radio vector barre iguales áreas en iguales tiempos""
Como ejemplo considere que el dibujo de la derecha representa la órbita de un satélite de la Tierra y haga que AB y CD sean porciones de la órbita cubiertas en 3 horas cerca del apogeo y del perigeo, respectivamente. Si O es el centro de la Tierra, las áreas sombreadas OAB y OCD son iguales. Lo que significa, obviamente, es que CD es más larga que AB, debido a que cerca del perigeo el satélite se mueve mucho más rápido y cubre en las 3 horas una distancia mayor. EnergíaLa energía se puede definir libremente como algo que puede hacer mover a una máquina. Las formas de energía que mueven nuestras máquinas son, normalmente, la electricidad o el calor; la luz es otra forma de energía, convertida en electricidad mediante células solares, que generan la potencia de la mayoría de los satélites. La gravedad también puede proveer energía. Las ruedas de los relojes de nuestros abuelos giraban por medio de pesos que descendían gradualmente hacia el fondo del reloj, en cuyo punto tenían que ser subidos de nuevo o el reloj se paraba. Thomas Jefferson, tenía en su casa cerca de Charlottesville, Virginia, un reloj cuyos pesos (colgados a un lado de la habitación) eran balas de cañón amarradas a una cuerda y para que el reloj tuviera cuerda para 7 días, había hecho un agujero en el suelo que permitía a las balas descender hasta el sótano. Cuando una bala o un peso se elevan contra la fuerza de la gravedad, adquieren energía potencial, energía en virtud de su posición, proporcional a la altura a que han sido elevados. Si se suelta el peso, pierde altura y energía potencial, pero gana velocidad y energía cinética, la energía debida a la velocidad del movimiento. La energía cinética se puede volver a convertir en potencial, como ocurre en la montaña rusa cuando pasa por el fondo de una depresión y sube de nuevo. Un cambio similar ocurre cuando se tira una piedra hacia arriba con una velocidad v. Si su masa es m (el concepto de masa se definirá más adelante, de momento véalo como algo relacionado con el peso), su energía cinética será: 1/2 mv2 Cuando sube, v y la energía cinética disminuyen, pero eso se compensa con el aumento de la energía potencial: h m g donde h es la altura en metros y g es una constante que mide la intensidad de la fuerza de la gravedad: si m está en kilogramos, h en metros y v en metros por segundo (escrito m/s ; la velocidad de una persona caminando es de 1-2 m/s), g es aproximadamente 9.81. La suma de las dos es la energía total E y permanece constante: E = 1/2 mv2 + h m g = constante Cuando la piedra sube, la parte cinética de su energía se hace cada vez menor, siendo cero cuando alcanza el punto más alto, donde, durante un breve instante v = 0. Durante el viaje de descenso, tiene lugar lo contrario. En una sección posterior volveremos a ver esta fórmula y el concepto de energía. Para un satélite de masa m que órbita la Tierra (o para un planeta alrededor del Sol) existe una fórmula similar: E = 1/2 mv2 – k m/r = constante Aquí k es otra constante, de hecho relacionada con g, porque ambas constantes reflejan la intensidad de la gravedad de la Tierra (el valor exacto es: k = gR2, donde R es el radio de la Tierra, en metros).
No deje que le confunda el signo menos: cuando el satélite se eleva, r aumenta, k m/r se hace menor, pero -k m/r se hace grande, es menos negativo que cerca de la Tierra. Esta ecuación indica porqué la velocidad del satélite disminuye cuando se aleja y aumenta cuando regresa. Suponga que el satélite tiene la velocidad suficiente para escapar completamente de la gravedad de la Tierra (la "velocidad de escape" V). Cuando esté lejos de la Tierra, donde k m/r es cercano a cero, su energía cinética tambien estará agotada, o sea, v = 0. Como la suma E es la misma en todas partes, esto da a entender que par una sonda espacial que justo por poco escapó de la gravedad de la Tierra, E = 0. Por esto V2 = 2k/R = 2 g R Con g = 9.81 y R =6 371 000 metros V
será unos 11200 m/s.
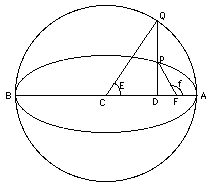
La Anomalía MediaAnteriormente se ha dicho que se necesitaba un tercer elemento orbital para especificar donde se localiza el satélite en su órbita. Puesto que la ecuación de la elipse orbital es r = a(1 – e2)/(1 + e cos f) cada valor del ángulo f llamado "anomalía verdadera", especifica una posición a lo largo de la órbita. Por consiguiente se puede usar la anomalía verdadera como tercer elemento orbital. La anomalía verdadera f varía periódicamente alrededor de la órbita, rápidamente cerca del perigeo y lentamente cerca del apogeo. La 2ª Ley de Kepler nos lo dice todo sobre esta variación y deberá permitirnos obtener una fórmula que dé la forma en que varía fconel tiempo t. Desgraciadamente, no existe una forma clara para expresar esa fórmula.
Siguiente Sección Opcional: #12a Más de la Segunda Ley de Kepler Mayores Detalles del Cálculo de Órbitas: #12b Cómo se Calcula el Movimiento de las Órbitas Siguiente Parada Regular: #13 Cómo Caen las Cosas Página principal en Español (índice)Autor y Curador: Dr. David P. Stern y complementada por Horacio Chávez
Última Actualización 25 de Octubre de 2004
|