(12a) Más Respecto a la Segunda Ley de Kepler

La Relación de Velocidades en Perigeo y Apogeo

    La segunda ley de Kepler describe la manera en que la velocidad v de un objeto orbitando un solo centro varía alrededor de su órbita:

Como se aprecia en la sección #12, esto significa que la velocidad del objeto V se incrementa cuando su distancia r se reduce, y viceversa.

    En dos puntos de la órbita las direcciones de r y v están perpendiculares una de la otra: en el punto P de máxima aproximación ("perihelio" para un planeta, "perigeo" para una satélite de la Tierra), y en punto A de máxima distancia ("afelio" o "apogeo"). Sean sus valores r₁ y V₁ en P, y r₂ y V₂ en A.

    Imagine un satélite terrestre, localizado en el perigeo P (vea dibujo). En un segundo, este habrá avanzado una distancia de V₁ metros (o cualquier unidad que se haya utilizado). Dado que esto es tan solo una pequeña parte de la órbita, no ocurre un gran error si, al calcular el área barrida por el radio r₁, lo reemplazamos con una línea recta. El área barrida es por tanto, un triángulo rectángulo largo y angosto con una altura r₁ y de base V₁ (más angosto de lo que podríamos dibujar aquí, de manera que el dibujo es para dar la idea).

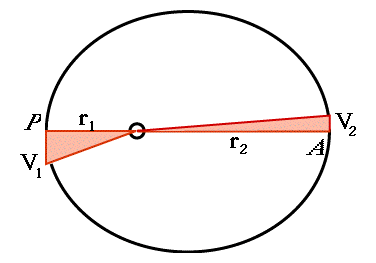
    El área A₁ de tal triángulo, de acuerdo a la fórmula del área de los triángulos rectángulos, es la mitad de la base multiplicada por la altura, o

    De manera similar, el área A₂ cubierta en un segundo después de pasar por el apogeo A es igual a:

Sin embargo, de acuerdo a la segunda ley de Kepler A₁ = A₂ de manera que

o, multiplicando todo por 2

Una manera más útil de esa relación ocurre si ambos lados se dividen entre V₂r₁ :

    La proporción de velocidades es igual a la inversa de la relación de las distancias. Entre más pequeña sea la distancia, más rápido será el movimiento. Si la distancia del perigeo es la mitad de la distancia del apogeo, la velocidad en ese lugar es el doble. (Pero por favor recuerde, esta proporcionalidad tan solo es válida con P y A, pero no lo es con ningún otro punto a lo largo de la órbita.)

¿Porqué son las Estaciones del Año Distribuídas Desigualmente?

    ¿Pero lo están?

    El equinoccio de primavera en el 2003 fue el 21 de Marzo, mientras que el equinoccio de otoño cayó el 22 de Septiembre, 184 días después. En el 2004, un año bisiesto, el equinoccio de primavera ocurrirá el 20 de Marzo, y si contamos los días, verá que para llegar allí se requieren tan solo 181 días. Los dos intervalos no son iguales.

    ¿Cómo puede ocurrir esto? Las posiciones del equinoccio están en lados opuestos de la órbita de la Tierra, a 180° de distancia., Aún así, para llegar al invierno (boreal) le toma 3 días más que para llegar al verano.

    De acuerdo a la segunda ley de Kepler, la tierra se mueve en su órbita un poco más rápido en el invierno. Como se vió al final de "Estaciones del Año" y también en conexión con la Teoría Milankovich de la edad de hielo, la Tierra está en su punto más cercano al sol, en el perihelio, alrededor del 4 de Enero. De acuerdo a la ecuación derivada aquí, es en ese momento cuando se mueve lo más rápido. Aún más, (vea el dibujo), la mitad de la elipse más cercana al Sol también es más pequeña. Con la Tierra la diferencia es pequeña, dado que la órbita es muy cercana a un círculo, pero existe de cualquier manera, y es la razón de la diferencia de los 3 días.

Nota: De acuerdo a un artículo relativo a Hiparco en "Wikipedia" (sección #4.4) la asimetría referida arriba era ya conocida por los antiguos Babilonios (Caldeos), y fue medida por Hiparco alrededor del año 140-130 A.C., y fue citada por Tolomeo.