Mapa del sitio

(12b) Como Se Calcula El Movimiento Orbital

(Sección Optativa)
        Esta sección está a un nivel superior que el resto, y se explica principalmente para usuarios avanzados, que pueden preguntarse como se deduce realmente el movimiento orbital. Para los demás proporciona un atisbo de la complejidad de los cálculos orbitales, ó, también,  puede saltarse. 

Como se dijo anteriormente, el movimiento de un satélite (o de un planeta) en su órbita elíptica está determinado por 3 "elementos orbitales": 

(1) El  semi-eje mayor a, la mitad de extenso que la elipse, que nos indica el tamaño de la órbita. 

(2) La excentricidad e, un número de 0 a 1, proporciona la forma de la órbita. Para un círculo: e = 0, valores mayores proporcionan progresivamente anillos más achatados, hasta  e = 1 donde la elipse se alarga hasta el infinito y se convierte en una parábola. Las órbitas de los grandes planetas son casi círculos: la de la Tierra, por ejemplo, tiene una  e = 0.0068

(3) La anomalía media M, un ángulo que crece a una razón constante, incrementándose en 360º cada órbita 

M = M(0) + 360°(t/T)

donde M(0) es el valor de M en el momento t = 0 y T es el período orbital. Determinados esos números, M se calcula fácilmente para cualquier momento t.

No obstante, la posición real de un satélite está dada por la anomalía verdadera  f. En las coordenadas polares (r, f) que describen el movimiento del satélite en su plano orbital,  f es el ángulo polar. La ecuación de la órbita es: 

r = a(1 – e2)/(1 + e cos f)

El ángulo  f  también se incrementa 360o cada órbita completa, pero no de forma uniforme. Por la ley de áreas de Kepler, crece más rápidamente cerca del perigeo (el punto más cercano a la Tierra)  y más lentamente cerca del apogeo (el punto más distante). 

La información necesaria para deducir  f para cualquier t está dentro de la ley de áreas, pero el cálculo real no es fácil. El proceso implica a un ángulo auxiliar, la  anomalía excéntrica E , la cual, al igual que  f y M se incrementa 360o cada órbita. En el perigeo, las tres anomalías son iguales a cero. 
 

El dibujo de la derecha proporciona una construcción geométrica de esos ángulos (no intente despiezarlo). La elipse orbital está encerrada en un círculo de radio a, y da la posición P del satélite, se puede dibujar un punto correspondiente Q en el círculo, compartiendo la misma línea  perpendicular al eje de la elipse. Luego E es el ángulo entre el eje mayor de la elipse y la línea dibujada desde el centro del círculo hasta Q ("excéntrico" puede significar aquí  "desde el centro").

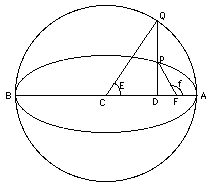
Ecuación de Kepler

Suponga dados los elementos a, e y M(0) en el momento t = 0  y necesitamos encontrar el valor de  f en un momento diferente t. Conociendo f, la ecuación citada anteriormente nos da  r,  y (r, f) juntos señalan la posición del satélite en su plano orbital. El primer paso es deducir 

M = M(0) + 360°(t/T)

Asumimos que es conocido el período T (esto requiere la 3ª ley que, para órbitas circulares, es abordada en las secciones 20 y 20a). Se puede evidenciar que el ángulo E satisface "la ecuación de Kepler" 

M = E – (180°/ π)e sen E

donde π = 3.14159256...es la relación entre la circunferencia de un círculo y su diámetro. Se puede preguntar ¿como aparece de repente ese número?. El hecho es que la división del círculo en 360º puede ser apropiada para su uso (lo heredamos de los antiguos babilonios) pero el número 360 no tiene un sitio específico en las matemáticas. Probablemente esté relacionado con el número de días del año. La división "natural" de los ángulos que se usa en cálculo y en otras ramas de las matemáticas es en radianes, donde 360º es igual a 2π = 6.2831... radianes (haciendo a cada radian igual a unos 57.3º). Con los ángulos medidos en radianes, la ecuación de Kepler se simplifica en 

M = E – e sen E

No importa que formato se use, las matemáticas no tienen ninguna fórmula que nos de E en términos de M. Sin embargo, a menudo las soluciones se pueden aproximar a algún grado de precisión por iteración, comenzando con una solución aproximada, luego mejorándola una y otra vez mediante un proceso de aproximación (un "algoritmo", vea aquí más información sobre esta palabra). Si la excentricidad e no es muy grande, la elipse no es muy diferente a un círculo y entonces M y E no son muy diferentes. Así, una conjetura inicial 

E' = M

no estará muy apartada. Poniendo esta conjetura dentro del término sen E da una suposición E"

E" = M + (180°/π)e sen E'

Se puede ahora introducir E" en el término sen E, obteniendo una mayor aproximación, y así en adelante... hasta que los primeros, digamos, diez decimales del valor de E no continúan cambiando. en este punto podemos decidir que ya tenemos una E  con suficiente precisión y para el proceso. Una computadora maneja este proceso de mejora continua ("iteración de la solución", una forma de algoritmo) muy rápidamente, también existen otros métodos, con la suficiente velocidad, aun cuando e no sea muy pequeña. 

Determinado E, un cierto número de fórmulas nos darán la anomalía verdadera f. Por ejemplo, se puede deducir primero 

r = a(1 – e cos E)

Y luego cos f se puede obtener de 

r = a(1 – e2)/(1 + e cos f)

y, a continuación, el sen f se puede obtener del cos f. Todo esto, hoy en día, se computa de forma fácil y automática, pero teníamos un gran lío en las épocas anteriores a la aparición de las computadoras. 

La Órbita en el Espacio
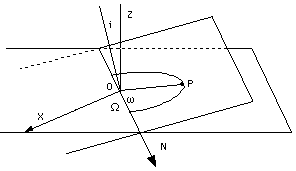Los 3 restantes elementos orbitales son ángulos que nos dan la posición de la órbita en 3 dimensiones. Están descritos abajo, pero su uso real pertenece a un curso universitario en mecánica orbital y se omitirá. Los ángulos: 
  1.  Inclinación i.
  2.  El argumento del perigeo ω (minúscula omega griega).
  3.  La longitud del nodo ascendente Ω (omega mayúscula).

Orientar la órbita en 3 dimensiones requiere un plano de referencia y una dirección de referencia. Para las órbitas de satélites, el plano de referencia, el plano horizontal en el dibujo, es, a menudo, el plano ecuatorial de la Tierra (a veces es el plano de la eclíptica). La dirección de referencia, en ambos casos  es la dirección desde el centro de la Tierra hacia el equinoccio de primavera (la cual pertenece a ambos planos superiores). Podremos llamarla la dirección x, ya que es su papel en las coordenadas (x,y,z) usadas en los cálculos orbitales. 

Dos planos no paralelos interseccionan siempre a lo largo de la línea, de la misma forma que el plano de una puerta intersecciona con el plano de la pared a lo largo del quicio de la puerta. El plano orbital y el ecuatorial (usados para referencia) hacen lo mismo, y su intersección se denomina la línea de nodos N. Haga que el origen O de nuestras coordenadas sea el centro de la Tierra, el cual es, también, el foco de la elipse; este punto pertenece a ambos planos, ecuatorial y orbital y está, por consiguiente también, en su línea de intersección N (dibujo).

Luego... 

  1. La inclinación i es el ángulo de apertura de la "bisagra" a lo largo de N. Se define mejor erigiendo en O líneas perpendiculares a cada plano y midiendo el ángulo entre ellas (dibujo).

    2.  
  2. El ángulo Ω se mide en el plano ecuatorial entre N y la dirección de referencia x. Podemos imaginar girando la "bisagra" N alrededor del punto O, sin cambio en la inclinación: el plano orbital  cubre todos los valores posibles de  Ω.

    3. Pero, ¿cual es el pequeño "nodo ascendente"?. La definición anterior contiene alguna ambigüedad: N define dos líneas saliendo de O en sentidos opuestos. ¿Desde cual de ellos se deberá medir Ω? Para resolver esto se debe observar que el plano del ecuador divide el espacio en dos partes, una al norte de él y otra al sur. Especificando "el nodo ascendente" se selecciona la rama que cruza el satélite cuando entra en la mitad norte del espacio, mejor que cuando la cruza al salir. 
     
  3. Finalmente, ω es el ángulo medido en el plano orbital entre N y la  dirección desde O hacia el punto de perigeo P. Si el perigeo coincide en la "bisagra", en la parte positiva de x, luego ω= 0; girando la órbita 90o hasta que la línea OP seaperpendicular a N hace ω = 90o, girándola más, hasta que alcance la parte negativa de x,  hace ω = 180o. 
Suponga que tiene los elementos orbitales de una satélite, por ejemplo la lanzadera espacial (puede obtenerla de la world-wide web). Los primeros tres (a, e, M), con M dado en un momento determinado, la permite calcular donde estará el satélite en cualquier momento en su órbita. Con (i, ω, Ω) puede, entonces, encontrar donde estará en el cielo.
        [Para quienes les gustaría conocer más acerca de la forma en que son calculadas dichas rotaciones en el espacio, vea problema 8 en el artículo "Ejercicios de Trigonometría." Ese problema tan solo trata con las rotaciones en dos dimensiones (e.g. sobre una hoja de papel), pero una peque–a sección adicional ligada al final de ese artículo explica como esto se extiende a 3 dimensiones.]

Página principal en Español (índice)


Linea del Tiempo               Glosario .

Siguiente Sección Opcional: #12c Método de Halley para Calcular la UA

Siguiente Parada Regular: #13 Cómo Caen las Cosas

Autor y Curador:   Dr. David P. Stern
     Correo al Dr. Stern:   stargaze("at" symbol)phy6.org   (Inglés, por favor).

Traducción al Espa–ol por J. Méndez

y complementada por Horacio Chávez

Última Actualización 13 de diciembre de 2001