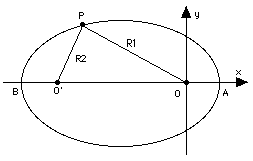
| Los dos puntos son denominados los focos de la elipse, y son
importantes aquí porque Kepler descubrió que el Sol siempre
ocupa un foco de la elipse orbital, no el centro, como se podría
pensar, p.e. el origen, donde la elipse está determinada por su
ecuación en un sistema de ejes perpendiculares (x,y).
(x2/a2) + (y2/b2) = 1
Los focos están siempre localizados a lo largo de uno
de los dos ejes simétricos de la elipse, los ejes (x,y) cuando se
usa la ecuación superior, el eje mayor de la elipse. Si a
es mayor que b, el eje mayor se sitúa al lo largo del eje
de las x, y lo decimos para mostrar que en este caso
R1 + R2 = 2a
[Pista: Haga un croquis de la elipse y los ejes que la definen, marque
uno de los puntos donde cruza el eje de las x y analice R1 y
R2 de este punto]. El valor de a en una órbita
elíptica se conoce en astronomía como el eje semi-mayor
y está considerado como uno de los seis elementos orbitales que definen el movimiento de acuerdo a las leyes de Kepler.
Murmullos en el Capitolio de los EE.UU.
Los focos de una elipse tienen una propiedad interesante. Un elipsoide
de revolución es una figura tridimensional obtenida rotando
una elipse alrededor de uno de sus ejes. Si se hace una elipsoide hueca
de esta figura y se platea su interior como si fuera un espejo,
y si una fuente luminosa se coloca en uno de sus focos, todos sus
rayos convergirán en el otro foco. Aunque solo se platee
una parte del elipsoide, toda la luz que llega a esa parte se concentrará
en el otro foco.
Las ondas sonoras también pueden comportarse como la luz.
La cámara del Capitolio de Washington en la que la Cámara
de Representantes acostumbran a reunirse tiene un techo de la forma de
un cuadrante (mitad de la mitad) de un elipsoide, con sus focos cerca del
suelo. Se hizo por razones arquitectónicas, hace unos 200 años,
pero permite a una persona en un foco lograr oir a cualquiera hablando
en el otro foco, hasta murmullos. Supuestamente, Daniel Webster se sentaba
en uno de estos lugares y hacía buen uso de su carácter especial.
Hoy en día la Cámara de Representantes tiene muchos
más miembros, usan cámaras mayores y su antigua sala de reuniones es un museo que exhibe estatuas de americanos distinguidos.
Cada año varios miles de visitantes son guiados s través
de la cámara. En algún momento durante su visita, se reúnen en ó cerca de un foco, identificado por una marca de bronce en el suelo, para escuchar los murmullos de su guía que está en el otro foco. Por cierto, un cuadro muy conocido de esta cámara, con las caras de sus ocupantes claramente identificables, fue hecha por Samuel Morse, el artista que también inventó el telégrafo eléctrico. Una copia de este cuadro y su historia se muestran en la sala.
|