 Figúrese que está de pie a una altura de h metros
sobre el océano y observa a lo ancho del agua. ¿Cual es la
distancia
D al horizonte? Se puede calcular si conoce el radio R
de la Tierra.
Figúrese que está de pie a una altura de h metros
sobre el océano y observa a lo ancho del agua. ¿Cual es la
distancia
D al horizonte? Se puede calcular si conoce el radio R
de la Tierra.
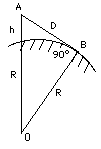
Su línea de visión hacia el horizonte es tangente a la Tierra, una línea que toca la esfera de la Tierra justo en un punto, indicado como B en el dibujo. Si O es el centro de la esfera, por un conocido teorema de geometría sabemos que la tangente es perpendicular al radio OB, o sea, forma un ángulo de 90º con el. Resulta que el triángulo OAB cumple el teorema de Pitágoras, que se puede escribir: (OA)2 = (AB)2 + (OB)2 o poniendo la longitud de cada línea con sus letras (R + h)2 = D2 + R2 Por una identidad algebraica (deducida en el "repaso de matemáticas"), el lado izquierdo es igual a: R2 + 2Rh + h2, dando R2 + 2Rh + h2 = D2 + R2 Si ahora restamos R2 de ambos lados de la igualdad y reordenamos los restantes términos de la izquierda h(2R + h) = D2 El diámetro 2R de la Tierra es mucho mayor que h y por consiguiente el error introducido si (2R+h) se reemplaza por 2R es muy, muy pequeño. Realizando esta sustitución tenemos 2Rh = D2 D = √(2Rh) donde √ indica "raiz cuadrada de". Esta ecuación nos deja calcular D, en kilómetros, si h y R están en kilómetros, además aún es posible simplificar: √(2Rh) = (√(2R)) x (√(h)) con las dos raíces multiplicadas. Usando R = 6371 km, √(2R) = 112.88, obteniendo D = 112.88 km √(h) Si está en lo alto de una montaña de 1 km de alta, h = 1 km, su horizonte debería estar a 112.88 km (omitimos la refracción de la luz en la atmósfera, que puede modificar este valor). Desde la cima del Mauna Kea en Hawaii, un volcán extinguido de 4 km de altura (también un lugar donde hay importantes observatorios astronómicos), el horizonte debería ser aprox. el doble de la distancia, 226 km. Por otro lado, de pie en la playa con sus a unos 2 metros = 0.002 km sobre el agua, como √(0.002) = 0.04472, el horizonte está solo a 5 km de distancia.
El cálculo debería también mantenerse desde el otro lado. Desde un bote en el océano debería comenzar a ver la cima del Mauna Kea desde una distancia de 226 km (de nuevo sin contar con la refracción). El 15 de noviembre de 1806, el teniente Zebulon Pike del ejercito de los EE,UU, capitanea un grupo de expedición a través de las llanuras del medio oeste de los EE.UU., viendo a través de sus binoculares la cima de una montaña lejana, justo sobre el horizonte. Su grupo necesitó una semana cubrir las 100 millas hasta la montaña, que se conoce ahora como Pike's Peak, una de las más altas de Colorado. Pike en realidad probó de escalar a su cumbre, pero la nieve y la inesperada altura le obligaron a regresar. |
