| La siguiente prueba de Aristarco fue observar cuando estaba la media
luna exacta iluminada por el Sol. Para que esto ocurra, el ángulo
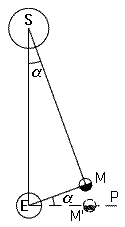
Tierra-Luna-Sol (ángulo EMS en el dibujo) deberá ser de 90º exactos.
Conociendo el movimiento del Sol a lo ancho del cielo, Aristarco podía
también localizar el punto P en el cielo, en la órbita de
la Luna (cerca de la eclíptica), el cual está exactamente
a 90º de la posición del Sol como lo vemos desde la Tierra.
Si el Sol estuviera muy lejos, la media luna estaría también en esa línea, en una posición como M' (dibujada a diferente escala para su claridad).
Aristarco estimó, no obstante, que la posición de la media
luna genera un pequeño ángulo a
con la posición de P de aproximadamente a 1/30 de un ángulo recto ó de 3º.
Como indica el dibujo, el ángulo ESM (Tierra-Sol-Luna) también es igual a 3º. Si Rs es la distancia del Sol y Rm la de la Luna, un círculo de 360° alrededor del sol a la distancia de la Tierra tiene una longitud de
2pRs
(p = 3.14159...). La distancia Rm = EM es casi tan larga como un arco de ese círculo, cubriendo solo 3°
ó 1/120 del círculo completo. Resulta que
Rm = 2pRs/120 ~Rs/19
Por consiguiente
Rs/Rm ~ 19
haciendo al Sol (de acuerdo con Aristarco) 19 veces más lejano
que la Luna. Dado que los dos tienen casi el mismo tamaño en el
cielo, aún cuando uno de ellos está 19 veces más lejano,
el Sol deberá tener, también, un diámetro19 veces
mayor que el de la Luna.
Si el diámetro de la Luna es la mitad del de la Tierra,
el Sol deberá ser 19/2 ó cerca de 10 veces más ancho
que la Tierra. El efecto descrito en la sección (8c) modifica este
argumento un poco (los detalles
aquí),
haciendo a la Tierra 3 veces más ancha que la Luna y no dos. Si
Aristarco había observado de forma correcta, eso debería
hacer al diámetro del Sol 19/3 veces, algo más de 6 veces,
el de la Tierra.
En realidad no es correcto. Su método no funciona realmente,
porque en realidad la posición de la media luna está muy
cercana a la línea OP. El ángulo p,
en vez de tener 3º, es normalmente tan pequeño que Aristarco
nunca pudo haberlo medido, especialmente sin un telescopio. La distancia
real al Sol es unas 400 veces mayor que la de la Luna, no19 veces, y el
diámetro del Sol es, igualmente, unas 400 veces mayor que el de
la Luna y más de100 veces el de la Tierra.
Pero no hay ninguna diferencia. La conclusión principal
de que el Sol es inmensamente mayor que la Tierra, aún se mantiene.
Aristarco pudo haber dicho justamente que el ángulo p
era a lo sumo de 3º, en cuyo caso el Sol estaría como
mínimo 19 veces más distante que la Luna y su tamaño
como
mínimo 19/3 veces mayor que la Tierra. De hecho pudo
decir eso, pero también aseveraba que era menos de 43/6 veces
mayor que la Tierra (los griegos usaban fracciones simples, ya que ellos
no sabían nada sobre los decimales), lo que estaba ampliamente fuera
de lugar. Pero no hay diferencias: con tal de que el Sol sea mucho mayor
que la Tierra, es más lógico que esté en el centro
y no que lo esté la Tierra.
Buena lógica, pero pocos la aceptaron, ni siquiera Hiparco ni
Tolemeo. Hicieron falta cerca de18 siglos para que la idea apareciera de
nuevo, en la mente de Copérnico. |