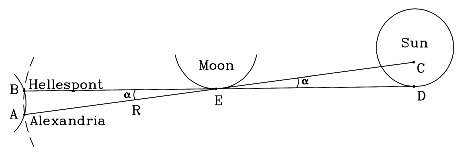
| En un eclipse total de Sol, la Luna apenas cubre el Sol. El Sol está
tan distante que cuando se le mira desde cualquier lugar de la Tierra,
cubre prácticamente la misma parcela de cielo, con una anchura de
unos 0.5º. Hiparco se fijó en el punto E del borde de la Luna
(dibujo), el punto que, durante la totalidad y cuando se veía
desde el Helesponto (punto B), se superponía justamente al punto
D del borde del Sol.
Visto desde Alejandría (punto A), en el mismo momento, el punto E solo se superponía al punto C del Sol, aprox. a 1/5 de diámetro solar separado del borde, por lo que no era un eclipse total. Un quinto del diámetro del Sol cubre solamente unos 0.1º del cielo, así que el pequeño ángulo a (alfa, A griega) entre las dos direcciones mide unos 0.1º. Este ángulo es el paralaje del borde de la Luna, vista desde los dos lugares citados arriba. Es improbable que Hiparco conociera la distancia AB, pero probablemente conocía las latitudes del Helesponto y Alejandría. La latitud local puede evidenciar ser igual a la elevación del polo celestial sobre el horizonte y actualmente se puede deducirse fácilmente observando la altura de la Polar, la estrella del polo sobre el horizonte. En los tiempos de Hiparco el polo de los cielos no estaba cerca de la Polar (debido a la precesión de los equinoccios), pero Hiparco, que había cartografiado la posición de unas 850 estrellas, debía conocer sus posiciones muy bien. La latitud del Helesponto (en un atlas moderno) es de 40° 20' (40 grados y 20 minutos, 60 minutos por grado), mientras que la de Alejandría es de 31° 20', una diferencia de 9°. Daremos por hecho que Alejandría está exactamente en el sur. Si, además, r es el radio de la Tierra, la circunferencia de la Tierra será 2pr, donde p = 3.1415926... ("pi", P minúscula griega) es la relación entre la circunferencia y el diámetro de un círculo. Puesto que la circunferencia es igual a 360º, tenemos AB = (2p r/360)· 9 el punto indica multiplicación (equivalente algebraico del símbolo x). La distancia R a la LunaLos puntos AB están también colocados en otro círculo, centrado en la Luna. El radio en este caso es la distancia R a la Luna y debido a que el arco AB cubre 0.1º, tenemosAB = (2pR/360)·0.1 Estrictamente hablando, cada uno de los dos arcos AB enunciados en las ecuaciones anteriores están medidos a lo largo de un círculo diferente, con radios diferentes (y los dos círculos curvados hacia lados opuestos). No obstante, en ambos casos AB cubre solo una pequeña parte del círculo, así que, como aproximación, podemos considerar que cada uno de los arcos son iguales a la distancia recta AB. Esta suposición nos permite estimar las dos expresiones como iguales y escribir (2p R/360)·0.1 = (2pr/360)·9 Multiplicando ambas igualdades por 360 y dividiéndolas por 2p nos da Dividiendo por (0.1 r) sugiere que la distancia a la Luna es de 90 radios terrestres, una sobrevaloración del 50%. Un cálculo más precis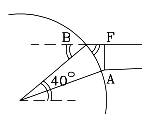o
Una razón de que se obtengan valores excesivos es que se da por hecho
que la Luna está arriba en lo alto en A o B. Realmente, es
muy probable que esté a un ángulo significativo con la dirección hacia arriba, el "cenit" (vea el dibujo).
Luego la sección cortada por el ángulo a del círculo de radio R alrededor de E no es AB, sino AF (segundo dibujo) que es menor. Tenerlo en cuenta reduce la distancia. No sabemos donde estaba el Sol durante el eclipse del 129 a.C., pero deberá estar en la eclíptica (¡Obviamente las palabras están relacionadas!), que lo coloca, en cualquier caso, dentro de los 23.5° del ecuador celestial. Asumiendo que estaba en el ecuador (esto es, pasó sobre el ecuador de la Tierra) y al sur de las observaciones descritas (p.e.: el eclipse ocurre cerca del mediodía) podemos hacer una tosca estimación de la corrección usando trigonometría sencilla (vea la sección M-8). El Helesponto está en una latitud de 40º y como indica el dibujo, es también el ángulo entre la dirección de la Luna y el cenit. Del dibujo (x indica multiplicación) Repitiendo el cálculo precedente para AF AF = 0.766 AB = 0.766·(2p r/ 360)·9 y al final
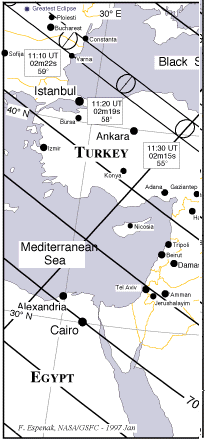
NotaAlgunos astrónomos han cuestionado si Hiparco utilizó el eclipse del a–o 128 AC--lo cual ocurrió durante su vida--o en lugar de eso utilizó registros de uno anterior en el a–o 190 AC, el cual también pasó cerca de un lugar llamado Helesponto, a lo largo de una ruta muy similar. Las rutas de esos eclipses y muchos otros se pueden encontrar en el atlas de eclipses de Fred Espenak, accesible desde la página de eclipses de la NASA, la cual es mantenida por él, enhttp://sunearth.gsfc.nasa.gov/eclipse/eclipse.html
Las rutas de los eclipses están en
Comentarios finalesSegún "A History of Astronomy" de A. Pannekoek, el resultado obtenido por Hiparco fue entre 62 y 73 radios terrestres. Hoy sabemos que la distancia media es de 60 radios, variando en algunos radios debido a la excentricidad de la órbita de la Luna.En ausencia de un cronometraje exacto, con el método casi está garantizado que se produzca una sobremedición. La tierra gira debajo del punto de sombra proyectado por la Luna, que hace que ese punto pase rápidamente sobre una larga banda; pasa sobre muchos lugares en momentos diferentes. El Helesponto fue uno de los muchos lugares donde el eclipse fue total. Igualmente, Alejandría fue uno de los muchos lugares donde solo cubrió las 4/5 partes del Sol. Seleccionando aleatoriamente el punto B del primer grupo y el punto A del segundo podemos tener una línea mayor que representa AB y una mayor (e incorrecta) distancia a la Luna. El hecho de que Alejandría está casi al sur del Helesponto no garantiza que su eclipse sea compartido o que no sea muy diferente. |
